Trang chủ
Đề thi & kiểm tra
Khác
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Cho hàm số y= f( x ) có bảng biến...
Cho hàm số y= f( x ) có bảng biến thiên: Tìm tất cả cá giá trị m để bất phương trình
Câu hỏi :
Cho hàm số \(y\, = \,f\left( x \right)\) có bảng biến thiên:
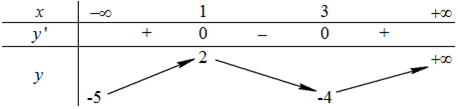
Tìm tất cả cá giá trị \(m\)để bất phương trình \(f\left( {\sqrt {x\, + \,1} \, + \,1} \right)\,\, \le \,\,m\)có nghiệm?
Cho hàm số \(y\, = \,f\left( x \right)\) có bảng biến thiên:

Tìm tất cả cá giá trị \(m\)để bất phương trình \(f\left( {\sqrt {x\, + \,1} \, + \,1} \right)\,\, \le \,\,m\)có nghiệm?
* Đáp án
* Hướng dẫn giải
Đáp án:
Phương pháp giải: - Đặt ẩn phụ tìm điều kiện của \(t\)(\(t \in D\))
- Xét hàm \(f(t)\)và lập bảng biến thiên trên \(D\)
- Bất phương trình \(f(t) \le m\)có nghiệm nếu \(\mathop {\min f(t) \le m}\limits_D \)
Giải chi tiết:
Đặt thì \(t \in (1; + \infty )\). Với \(x = 3\) thì \(t = 3\)
Bảng biến thiên của \(f(t)\):
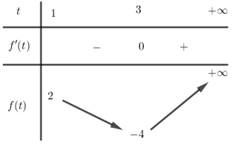
Do bất phương trình \(f(t) \le m\)có nghiệm khi và chỉ khi
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
