Cho hàm số y = f( x ) liên tục và có đạo hàm trên R. Hàm số y = f'( x ) có bảng xét dấu như bảng bên dưới. Bất phương trình
Câu hỏi :
Cho hàm số \(y\, = \,f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Hàm số \(y\, = \,f'\left( x \right)\) có bảng xét dấu như bảng bên dưới.
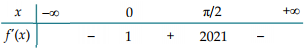
Bất phương trình \(f\left( x \right)\, > \,{e^{\cos x}}\, + \,m\) có nghiệm \(x\, \in \,\left( {0\,;\,\frac{\pi }{2}} \right)\) khi và chỉ khi
Cho hàm số \(y\, = \,f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Hàm số \(y\, = \,f'\left( x \right)\) có bảng xét dấu như bảng bên dưới.
Bất phương trình \(f\left( x \right)\, > \,{e^{\cos x}}\, + \,m\) có nghiệm \(x\, \in \,\left( {0\,;\,\frac{\pi }{2}} \right)\) khi và chỉ khi
* Đáp án
* Hướng dẫn giải
Đáp án:
Phương pháp giải: - Cô lập \(m\)đưa bất phương trình về dạng \(g(x) \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Rightarrow m \le \mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
- Lập luận để chứng minh \(g(x)\)đơn điệu trên \(\left( {0;\frac{\pi }{2}} \right)\)và suy ra \(\mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
Giải chi tiết:
Ta có:
\(f(x) > {e^{\cos x}} + m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Leftrightarrow f(x) - {e^{\cos x}} \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
Đặt \(g(x) = f(x) - {e^{\cos x}}\) \( \Rightarrow g(x) \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Rightarrow m \le \mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
Xét hàm số \(g(x) = f(x) - {e^{\cos x}}\)với \(x \in \left( {0;\frac{\pi }{2}} \right)\)ta có: \(g'(x) = f'(x) + \sin x.{e^{\cos x}}\)
Với \(x \in \left( {0;\frac{\pi }{2}} \right)\)ta có \(\sin x \in (0;1)\) \( \Rightarrow \sin x.{e^{\cos x}} > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Dựa vào BBT ta thấy \(f'(x) > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Do đó \(g'(x) > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\),do đó hàm số đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right]\)
\(\mathop { \Rightarrow \min g(x)}\limits_{\left[ {0;\frac{\pi }{2}} \right]} \) \( = g(0) = f(0) - e\)
\( \Rightarrow \mathop {\min g(x)}\limits_{\left( {0;\frac{\pi }{2}} \right)} \) \( > \mathop {\min g(x) = f(0) - e}\limits_{\left[ {0;\frac{\pi }{2}} \right]} \)
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
