Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng
Câu hỏi :
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng \(a\) và diện tích đáy bằng \({a^2}\) (tham khảo hình bên dưới). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng:
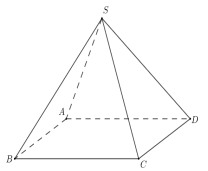
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng \(a\) và diện tích đáy bằng \({a^2}\) (tham khảo hình bên dưới). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng:

* Đáp án
* Hướng dẫn giải
Đáp án:
Phương pháp giải: - Đổi \(d(A;(SBC))\)sang \(d(O;(SBC))\)với \(O = AC \cap BD\)
- Gọi \(M\)là trung điểm của \(BC\),trong \((SOM)\)kẻ \(OH \bot SM\)chứng minh \(OH \bot (SBC)\)
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách
Giải chi tiết:
Ta có: \(AO \cap (SBC) = C \Rightarrow \frac{{d(A;(SBC))}}{{d(O;(SBC))}} = \frac{{AO}}{{OC}} = 2\)
\( \Rightarrow d(A;(SBC)) = 2d(O;(SBC))\)
Gọi \(M\)là trung điểm của \(BC\),trong \((SOM)\)kẻ \(OH \bot SM\)ta có:
\(\left\{ {\begin{array}{*{20}{c}}{BC \bot OM}\\{BC \bot SO}\end{array}} \right. \Rightarrow BC \bot (SOM) \Rightarrow BC \bot OH\)
\(\left\{ {\begin{array}{*{20}{c}}{OH \bot BC}\\{OH \bot SM}\end{array}} \right. \Rightarrow OH \bot (SBC) \Rightarrow d(O;(SBC)) = OH\)
Vì \({S_{ABCD}} = {a^2} \Rightarrow BC = a,OM = \frac{1}{2}AB = \frac{1}{2}BC = \frac{a}{2}\)
Ta có:
Xét tam giác vuông \(SOM\): \(OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \frac{{\frac{{a\sqrt 2 }}{2}.\frac{a}{2}}}{{\sqrt {\frac{{{a^2}}}{2} + \frac{{{a^2}}}{4}} }} = \frac{{a\sqrt 6 }}{6}\)
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
