Cho hình chóp đều S.ABC. Mặt phẳng

* Hướng dẫn giải

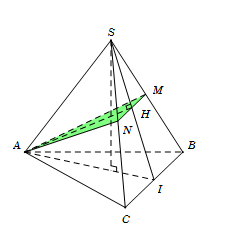
Gọi I là trung điểm BC.

Trong tam giác SAI kẻ \[AH \bot SI\;(H \in SI).\]

Trong tam giác SBC, qua H kẻ đường song song với BC, cắt SC ở MM, cắt SB ở N.

Qua cách dựng ta có \[BC\parallel \left( {AMN} \right).\,\,\left( 1 \right)\]

Và

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{SI \bot AH}\\{SI \bot MN(do\,SI \bot BC)}\end{array}} \right. \Rightarrow SI \bot (AMN)\\ \Rightarrow (SBC) \bot (AMN).\end{array}\)

Từ (1) và (2), suy ra thiết diện cần tìm là tam giác AMN.

Dễ thấy H là trung điểm của MN mà \[AH \bot \left( {SBC} \right)\] suy ra \[AH \bot MN\]. Tam giác AMN có đường cao AH vừa là trung tuyến nên nó là tam giác cân đỉnh A.

Đáp án cần chọn là: B