Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB=2a,AD=DC=a; cạnh bên SA=a và vuông góc với đáy. Mặt phẳng

* Hướng dẫn giải

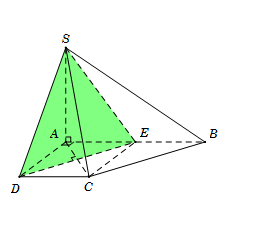
Gọi E là trung điểm AB.

Suy ra AECD là hình vuông nên \[DE \bot AC\].         (1)

Mặt khác\[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot DE\,\,\left( 2 \right)\]

Từ (1) và (2),  suy ra\[DE \bot \left( {SAC} \right) \Rightarrow \left( {SDE} \right) \bot \left( {SAC} \right)\]

Ta có\(\left. {\begin{array}{*{20}{c}}{(SDE) \supset SD}\\{(SDE) \bot (SAC)}\end{array}} \right\} \Rightarrow (\alpha ) \equiv (SDE)\)

Vậy thiết diện là tam giác SDE

Ta có\[SD = \sqrt {S{A^2} + D{A^2}} = a\sqrt 2 ;SE = \sqrt {S{A^2} + A{E^2}} = a\sqrt 2 \]

\[DE = AC = DC\sqrt 2 = a\sqrt 2 \]

Do đó tam giác SDE đều có cạnh\[a\sqrt 2 \]  nên \[{S_{{\rm{\Delta }}{\kern 1pt} SDE}} = \frac{{S{D^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\]Đáp án cần chọn là: C