Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng

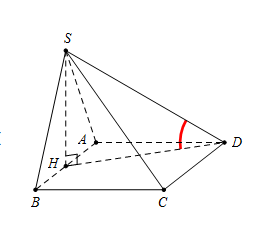
Gọi H là trung điểm của AB, tam giác SAB đều \[ \Rightarrow \,\,SH \bot AB.\]

Mà\[\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)\] và \[SH = \frac{{a\sqrt 3 }}{2}\]Suy ra\[\widehat {(SD;\left( {ABCD} \right))} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH} = {30^0}\]

Tam giác SHD vuông tại H, có\[\tan \widehat {SDH} = \frac{{SH}}{{HD}} \Rightarrow HD = \frac{{3a}}{2}.\]

Tam giác AHD vuông tại A, có\[AD = \sqrt {H{D^2} - A{H^2}} = a\sqrt 2 .\]

Vậy diện tích hình chữ nhật ABCD là\[{S_{ABCD}} = \sqrt 2 \,{a^2}.\]