Tìm tất cả các giá trị thực của m để phương trình

TXĐ : D=R.

\[2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m \Leftrightarrow {\log _2}{\left| x \right|^2} + {\log _2}\left| {x + 3} \right| = m\]

\[ \Leftrightarrow {\log _2}\left( {{{\left| x \right|}^2}.\left| {x + 3} \right|} \right) = m \Leftrightarrow {\left| x \right|^2}.\left| {x + 3} \right| = {2^m}\]

\[ \Leftrightarrow {x^2}.\left| {x + 3} \right| = {2^m}\]

Xét hàm\[f(x) = {x^2}.\left| {x + 3} \right|\]Ta có : \[f(x) = {x^2}.\left| {x + 3} \right| = \left| {{x^3} + 3{x^2}} \right|\]

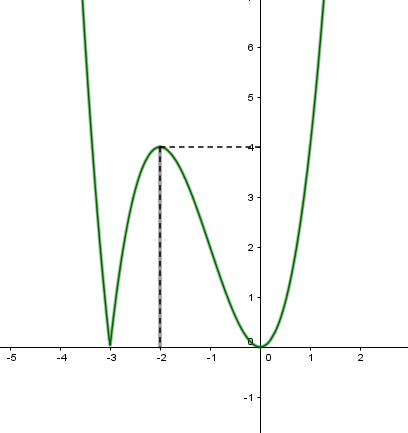
Để phương trình có 3 nghiệm phân biệt thì \[{2^m} = 4 \Leftrightarrow m = 2\]