Tập nghiệm của bất phương trình
Câu hỏi :
Tập nghiệm của bất phương trình \[\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\] là:
A.\[\left( {1;2} \right) \cup \left( {3; + \infty } \right)\]
B. \[\left( { - \infty ;1} \right) \cup \left( {2;3} \right)\]
C. \[\left( {1;2} \right) \cap \left( {3; + \infty } \right)\]
D. \[\left( { - \infty ;1} \right) \cap \left( {2;3} \right)\]
* Đáp án
* Hướng dẫn giải
\[\begin{array}{*{20}{l}}\begin{array}{l}\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1 > 1\end{array}\\{ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) > 0}\end{array}\]
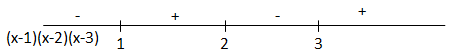
\[ \Rightarrow x \in (1;2) \cup (3; + \infty )\]
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bất phương trình logarit !!
Số câu hỏi: 35
Copyright © 2021 HOCTAP247
