Giải bất phương trình log 0 , 7 ( log 6 x^2 + x / x + 4 ) < 0

* Hướng dẫn giải

\[{\log _{0,7}}({\log _6}\frac{{{x^2} + x}}{{x + 4}}) < 0\]

Đkxđ: \(\left\{ {\begin{array}{*{20}{c}}{{{\log }_6}\frac{{{x^2} + x}}{{x + 4}} > 0}\\{\frac{{{x^2} + x}}{{x + 4}} > 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 4 < x < - 2}\\{x > 2}\end{array}} \right.\left( * \right)\)</>

\(lo{g_6}\frac{{{x^2} + x}}{{x + 4}} > 0,{7^0} = 1 \Leftrightarrow \frac{{{x^2} + x}}{{x + 4}} > 6 \Leftrightarrow \frac{{{x^2} + x}}{{x + 4}} - 6 > 0\)

\( \Leftrightarrow \frac{{{x^2} - 5x - 24}}{{x + 4}} > 0 \Leftrightarrow \frac{{(x - 8)(x + 3)}}{{x + 4}} > 0\)

Xét dấu\[f\left( x \right) = \frac{{(x - 8)(x + 3)}}{{x + 4}}\]

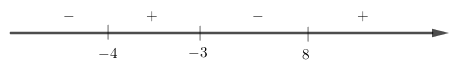
Vậy\[ - 4 < x < - 3\]  hoặc\[x > 8\]</>

Kết hợp với điều kiện ta được −4<x<−3 hoặc x>8.</x

Đáp án cần chọn là: A