Trang chủ
Đề thi & kiểm tra
Khác
Ứng dụng tích phân để tính diện tích !!
Cho hình vuông ABCD tâm O, độ dài cạnh là...
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình...
Câu hỏi :
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
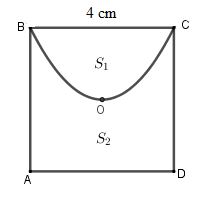
Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).

Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:
A.\(\frac{1}{2}\)
B. \[\frac{3}{5}\]
C. \[\frac{2}{5}\]
D. \[\frac{1}{3}\]
* Đáp án
* Hướng dẫn giải
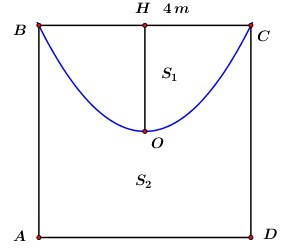
Gọi H là trung điểm của BC.
\[\begin{array}{*{20}{l}}{{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.}\\{{S_{ABCD}} = {4^2} = 16}\\{ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.}\\{ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.}\end{array}\]
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Ứng dụng tích phân để tính diện tích !!
Số câu hỏi: 27
Copyright © 2021 HOCTAP247
