Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức

Ta có:\[z = - 1 + 2i\] có điểm biểu diễn là\[M\left( { - 1;\,\,2} \right).\]

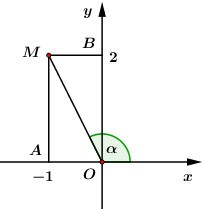
Ta có:\[\tan AOM = \frac{{AM}}{{OA}} = \frac{2}{1} = 2.\]

\[ \Rightarrow \tan \alpha = - \tan AOM = - 2\] (hai góc bù nhau)

\[ \Rightarrow \tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \frac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \frac{4}{3}\]