Cho hình chóp S.ABCD có

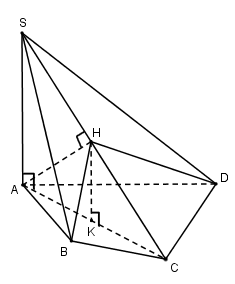
Ta có:\[SA \bot \left( {ABCD} \right) \Rightarrow AC\] là hình chiếu của SC trên

\[\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\]

\[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow {\rm{\Delta }}SAC\]vuông tại A và\[\widehat {SCA} = {60^0}\]

Xét tam giác vuông SAC có:

\[SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3 = a\sqrt 6 ;\,SC = \frac{{AC}}{{{\rm{cos}}60}} = \frac{{a\sqrt 2 }}{{\frac{1}{2}}} = 2a\sqrt 2 \]

Áp dụng hệ thức lượng trong tam giác vuông SAC có:

\[A{C^2} = HC.SC \Rightarrow \frac{{HC}}{{SC}} = \frac{{A{C^2}}}{{S{C^2}}} = \frac{{2{a^2}}}{{8{a^2}}} = \frac{1}{4}\]

Trong (SAC)  kẻ\[HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\]

Ta có:\[\frac{{HK}}{{SA}} = \frac{{HC}}{{SC}} = \frac{1}{4} \Rightarrow HK = \frac{1}{4}SA = \frac{{a\sqrt 6 }}{4}\]

Vậy\[{V_{H.ABCD}} = \frac{1}{3}HK.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 6 }}{4}.\frac{{3{a^2}}}{2} = \frac{{{a^3}\sqrt 6 }}{8}\]