Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
Câu hỏi :
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
A.\[V = \frac{{5{a^3}\sqrt 3 }}{{12}}\]
B. \[V = \frac{{{a^3}\sqrt 3 }}{{12}}\]
C. \[V = \frac{{{a^3}\sqrt 5 }}{{12}}\]
D. \[V = \frac{{{a^3}\sqrt 3 }}{{10}}\]
* Đáp án
* Hướng dẫn giải

Gọi O là trọng tâm tam giác đều ABC
Vì chóp S.ABC đều nên\[SO \bot \left( {ABC} \right)\]
⇒OA là hình chiếu vuông góc của SA lên (ABC)
\[ \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;OA} \right)} = \widehat {SAO} = {60^0}\]
\[SO \bot \left( {ABC} \right) \Rightarrow SO \bot OA \Rightarrow {\rm{\Delta }}SAO\] vuông tại O
Gọi D là trung điểm của BC ta có: \[AD = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AD = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow SO = AO.\tan 60 = \frac{{a\sqrt 3 }}{3}.\sqrt 3 = a\]
Vì tam giác ABC đều nên\[{S_{{\rm{\Delta }}ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]
Vậy\[{V_{S.ABC}} = \frac{1}{3}SO.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}a\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\]
Đáp án cần chọn là: BCâu 14. Cho hình chóp đều S.ABCD có diện tích đáy là 16cm2, diện tích một mặt bên là \[8\sqrt 3 c{m^2}\]. Thể tích khối chóp S.ABCD là:
A.\[\frac{{32\sqrt 2 }}{3}c{m^3}\]
B. \[\frac{{32\sqrt {13} }}{3}c{m^3}\]
C. \[\frac{{32\sqrt {11} }}{3}c{m^3}\]
D. \[4c{m^3}\]Trả lời:
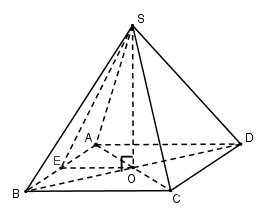
Gọi\[O = AC \cap BD\].Vì chóp S.ABCD đều nên\[SO \bot \left( {ABCD} \right)\]
Vì chóp S.ABCD đều nên ABCD là hình vuông
\[ \Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD\]
Gọi E là trung điểm của AB⇒OE là đường trung bình của tam giác ABD
\[ \Rightarrow OE//AD \Rightarrow OE \bot AB\]và \[OE = \frac{1}{2}AD = \frac{1}{2}.4 = 2\left( {cm} \right)\]
\(\left. {\begin{array}{*{20}{c}}{OE \bot AB}\\{SO \bot AB(SO \bot (ABCD))}\end{array}} \right\} \Rightarrow AB \bot (SOE) \Rightarrow AB \bot SE\)
\[ \Rightarrow {S_{{\rm{\Delta }}SAB}} = \frac{1}{2}SE.AB = 8\sqrt 3 \Rightarrow SE = \frac{{16\sqrt 3 }}{{AB}} = \frac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)\]
\[SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow {\rm{\Delta }}SOE\] vuông tại O
\[ \Rightarrow SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {48 - 4} = \sqrt {44} = 2\sqrt {11} \left( {cm} \right)\]
Vậy\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.2\sqrt {11} .16 = \frac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)\]
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Thể tích của khối chóp !!
Copyright © 2021 HOCTAP247
