Cho tứ diện đều ABCD có cạnh bằng 8. Ở bốn đỉnh tứ diện, nguời ta cắt đi các tứ diện đều bằng nhau có cạnh bằng x, biết khối đa diện tạo thành sau khi cắt có thể tích bằng ( frac{3...

* Hướng dẫn giải

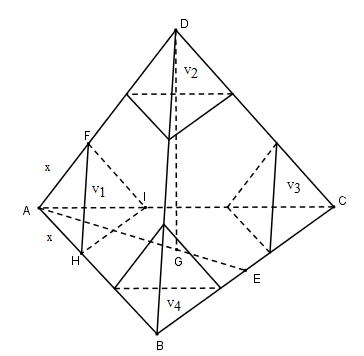
Tứ diện ABCD đều cạnh a có thể tích là \[{V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}\]

Vì tứ diện đều ABCD cạnh 8  nên\[{V_{ABCD}} = \frac{{{8^3}\sqrt 2 }}{{12}} = \frac{{128\sqrt 2 }}{3}\]

Tứ diện đều FAHI cạnh x nên\[{V_1} = \frac{{{x^3}\sqrt 2 }}{{12}}\]

Tương tự ta có:\[{V_2} = {V_3} = {V_4} = \frac{{{x^3}\sqrt 2 }}{{12}}\]

⇒Khối đa diện tạo thành sau khi cắt có thể tích là

\[V = {V_{ABCD}} - 4{V_1} = \frac{{128\sqrt 2 }}{3} - 4\frac{{{x^3}\sqrt 2 }}{{12}} = \frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3}\]

Vì khối đa diện tạo thành sau khi cắt có thể tích bằng\[\frac{3}{4}\]thể tích tứ diện ABCDABCD nên ta có:

\[\frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3} = \frac{3}{4}\frac{{128\sqrt 2 }}{3} \Rightarrow 128 - {x^3} = 96 \Leftrightarrow {x^3} = 32 \Rightarrow x = \sqrt[3]{{32}} = 2\sqrt[3]{4}\]

Đáp án cần chọn là: D