Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA=a. Điểm M thuộc cạnh SA sao cho

* Hướng dẫn giải

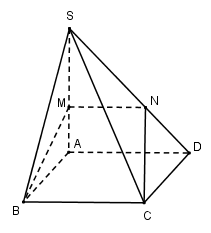
Vì\[BC//AD\]nên mặt phẳng (BMC) cắt (SAD) theo đoạn thẳng\[MN//AD\left( {N \in SD} \right)\]

Vì\[MN//AD \Rightarrow \frac{{SM}}{{SA}} = \frac{{SN}}{{SD}} = k\]

\[\begin{array}{*{20}{l}}{\frac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} = k \Rightarrow {V_{S.MBC}} = k.{V_{S.ABC}} = \frac{k}{2}.{V_{S.ABCD}}}\\{\frac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SD}} = {k^2} \Rightarrow {V_{S.MNC}} = {k^2}.{V_{S.ADC}} = \frac{{{k^2}}}{2}.{V_{S.ABCD}}}\\{ \Rightarrow {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\frac{k}{2} + \frac{{{k^2}}}{2}} \right){V_{S.ABCD}}}\end{array}\]

Để mặt phẳng (BMNC) chia hình chóp thành 2 phần có thể tích bằng nhau thì

\[\frac{k}{2} + \frac{{{k^2}}}{2} = \frac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \frac{{ - 1 + \sqrt 5 }}{2}\]do k > 0.

Đáp án cần chọn là: B