Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạnh AB,BC. Điểm I thuộc đoạn SA. Biết mặt phẳng (MNI) chia khối chóp S.ABCD thành hai ph...

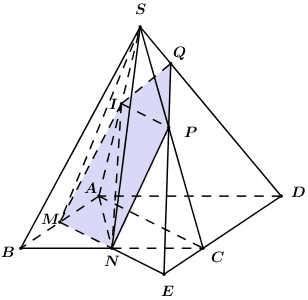
Giả sử\[SC \cap \left( {IMN} \right) = \left\{ P \right\} \Rightarrow \left( {IMN} \right) \cap \left( {SAC} \right) = IP\]

Ta có:\(\left\{ {\begin{array}{*{20}{c}}{(IMN) \cap (SAC) = IP}\\{(IMN) \cap (ABCD) = MN}\\{(SAC) \cap (ABCD) = AC}\end{array}} \right. \Rightarrow IP\parallel MN\parallel AC\)

Trong (ABCD) gọi \[\left\{ E \right\} = MN \cap CD\]trong (SCD) gọi \[Q = NP \cap SD\]

Khi đó thiết diện của hình chóp cắt bởi (MNI) là ngũ giác IMNPQ.

Gọi\[SM \cap \left( {ABCD} \right) = E \Rightarrow \frac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \frac{{ME}}{{SE}} = \frac{{11}}{{35}}\]theo bài ra ta có\[\frac{{{V_2}}}{{{V_1}}} = \frac{{{V_{M.ACD}}}}{{{V_{S.ABCD}}}} = \frac{{\frac{1}{3}.d\left( {M;\left( {ABCD} \right)} \right).{S_{ACD}}}}{{\frac{1}{3}.d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \frac{{11}}{{35}}.\frac{1}{2} = \frac{{11}}{{70}}\]

Ta có \[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]

Đặt\[\frac{{SI}}{{SA}} = x\,\,\,(0 < x < 1)\]áp dụng định lí Ta-lét ta có\[\frac{{SI}}{{SA}} = \frac{{SP}}{{SC}} = x\]

- Xét khối chóp S.BMN và S.ABCD:

  + Có cùng chiều cao (cùng bằng khoảng cách từ SS đến (ABCD).

\[{S_{BMN}} = \frac{1}{4}{S_{ABC}} = \frac{1}{8}{S_{ABC}}\](do tam giác BMNBMN và tam giác BACBAC đồng dạng theo tỉ số\[DH \bot \left( {ABC} \right)\])

Do đó\[{V_{S.BMN}} = \frac{1}{8}{V_{S.ABCD}} = \frac{1}{8}V\]

- Xét khối chóp S.IMN và S.AMN:

\[\frac{{{V_{S.IMN}}}}{{{V_{S.AMN}}}} = \frac{{SI}}{{SA}} = x \Rightarrow {V_{S.IMN}} = x.{V_{S.AMN}}\]

Ta có\[{S_{AMN}} = {S_{BMN}} = \frac{1}{8}{S_{ABCD}} \Rightarrow {V_{S.AMN}} = \frac{1}{8}V \Rightarrow {V_{S.IMN}} = \frac{x}{8}V\]

- Xét khối chóp S.INP và S.ANC:

\[\frac{{{V_{S.INP}}}}{{{V_{S.ANC}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}} = {x^2} \Rightarrow {V_{S.IMN}} = {x^2}.{V_{S.ANC}}\]

Ta có\[{S_{ANC}} = \frac{1}{2}{S_{ABC}} = \frac{1}{4}{S_{ABCD}} \Rightarrow {V_{S.ANC}} = \frac{1}{4}V \Rightarrow {V_{S.IMN}} = \frac{{{x^2}}}{4}V\]

- Xét khối chóp S.IPQ và S.ACD:\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}}\]

Ta có AMEC là hình bình hành nên\[EC = AM = \frac{1}{2}CD \Rightarrow \frac{{EC}}{{ED}} = \frac{1}{3}\]

Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến EPQ ta có:

\[\frac{{PS}}{{PC}}.\frac{{EC}}{{ED}}.\frac{{QD}}{{QS}} = 1 \Rightarrow \frac{x}{{1 - x}}.\frac{1}{3}.\frac{{QD}}{{QS}} = 1\]

\[\begin{array}{*{20}{l}}{ \Rightarrow \frac{{QD}}{{QS}} = \frac{{3\left( {1 - x} \right)}}{x} \Rightarrow \frac{{SQ}}{{QD}} = \frac{x}{{3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SQ + QD}} = \frac{x}{{x + 3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SD}} = \frac{x}{{3 - 2x}}}\end{array}\]

Suy ra\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = {x^2}.\frac{x}{{3 - 2x}} = \frac{{{x^3}}}{{3 - 2x}}\]

\[ \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{3 - 2x}}{V_{S.ACD}}\]

Mà\[{S_{ACD}} = \frac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.ACD}} = \frac{1}{2}V \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\]

Khi đó ta có:

\[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]

\[ \Rightarrow {V_1} = \frac{1}{8}V + \frac{x}{8}V + \frac{{{x^2}}}{4}V + \frac{{{x^3}}}{{2(3 - 2x)}}V\]

\[\begin{array}{l} \Rightarrow {V_1} = \left( {\frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}}} \right)V = \frac{7}{{32}}V\\ \Rightarrow \frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}} = \frac{7}{{32}}\\ \Leftrightarrow \frac{{1 + x + 2x2}}{4} + \frac{{{x^3}}}{{3 - 2x}} = \frac{7}{{16}}\\ \Leftrightarrow (1 + x + 2{x^2}).(12 - 8x) + 16{x^3} = 7(3 - 2x)\\ \Leftrightarrow 12 + 12x + 24{x^2} - 8x - 8{x^2} - 16{x^3} + 16{x^3} = 21 - 14x\\ \Leftrightarrow 16{x^2} + 18x - 9 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{3}{8}\left( {tm} \right)}\\{x = - \frac{3}{2}\left( {ktm} \right)}\end{array}} \right.\end{array}\]

\[ \Rightarrow \frac{{SI}}{{SA}} = \frac{3}{8} \Rightarrow \frac{{IS}}{{IA}} = \frac{3}{5} \Rightarrow \frac{{IA}}{{IS}} = \frac{5}{3}\]