Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng

* Hướng dẫn giải

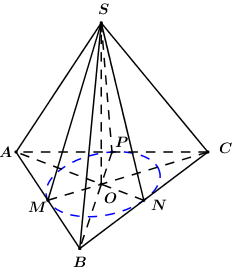
Gọi M,N,P lần lượt là hình chiếu của điểm SS lên AB,BC,AC ta có:

\[\begin{array}{*{20}{l}}{\,\,\,\,\,{S_{{\rm{\Delta }}ABC}} = {S_{{\rm{\Delta }}BCA}} = {S_{{\rm{\Delta }}CAB}}}\\{ \Rightarrow \frac{1}{2}SM.AB = \frac{1}{2}SN.BC = \frac{1}{2}SP.CA}\end{array}\]

Mà\[AB = BC = CA\,\,\left( {gt} \right) \Rightarrow SM = SN = SP\]

Gọi O là hình chiếu của S lên (ABC), ta có:

\(\left\{ {\begin{array}{*{20}{c}}{AB \bot SM}\\{AB \bot SO}\end{array}} \right. \Rightarrow AB \bot (SOM) \Rightarrow AB \bot OM\)

CMTT ta có\[ON \bot BC,\,\,OP \bot AC\]

Xét các tam giác vuông\[{\rm{\Delta }}SOM,\,\,{\rm{\Delta }}SON,\,\,{\rm{\Delta }}SOP\]có:

\[\begin{array}{*{20}{l}}{SO\,\,chung}\\{SM = SN = SP\,\,\left( {cmt} \right)}\end{array}\]

\[ \Rightarrow {\rm{\Delta }}SOM = {\rm{\Delta }}SON = {\rm{\Delta }}SOP\](cạnh huyền – cạnh góc vuông)

\[ \Rightarrow OM = ON = OP\] suy ra O cách đều các cạnh AB,BC,CA nên OO là tâm đường tròn nội tiếp \[{\rm{\Delta }}ABC\]hoặc O là tâm đường tròn bàng tiếp\[{\rm{\Delta }}ABC\]

+ TH1: O là tâm đường tròn nội tiếp\[{\rm{\Delta }}ABC\] Mà\[{\rm{\Delta }}ABC\]đều nên O là đồng thời là trọng tâm tam giác đều ABC. Khi đó ta có

\[AN = \frac{{\sqrt 6 .\sqrt 3 }}{2} = \frac{{3\sqrt 2 }}{2},\,\,AO = \frac{2}{3}AN = \sqrt 2 \]

\[ \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {18 - 2} = 4\]

\[{S_{{\rm{\Delta }}ABC}} = {\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\]

\[ \Rightarrow {V_{S.ABC}} = \frac{1}{3}SO.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}.4.\frac{{3\sqrt 3 }}{2} = 2\sqrt 3 \]

TH2: O là tâm đường tròn bàng tiếp \[\Delta ABC\].

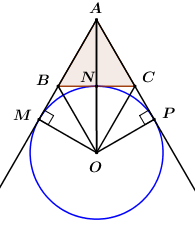
Gọi R là bán kính đường tròn bàng tiếp tam giác ABC, p là nửa chu vi tam giác ABC

\[ \Rightarrow p = \frac{{3\sqrt 6 }}{2}\]

Khi đó ta có\[{S_{ABC}} = \left( {p - BC} \right).R\]

\[ \Rightarrow {\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = \left( {\frac{{3\sqrt 6 }}{2} - \sqrt 6 } \right).R \Leftrightarrow R = \frac{{3\sqrt 2 }}{2}\]

Có\[AN = \frac{{\sqrt 6 .\sqrt 3 }}{2} = \frac{{3\sqrt 2 }}{2} \Rightarrow OA = AN + ON = 3\sqrt 2 \]

\[ \Rightarrow SA > OA = 3\sqrt 2 \] (quan hệ giữa đường vuông góc và đường xiên)

\[ \Rightarrow SB = 3\sqrt 2 \]

Áp dụng định lí Pytago trong tam giác vuông OBM có:

\[OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 6 }}{2}} \right)}^2}} = \sqrt 6 \]

Áp dụng định lí Pytago trong tam giác vuông SOB có:

\[SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\left( {\sqrt 6 } \right)}^2}} = 2\sqrt 3 \]

Khi đó ta có\[{V_{S.ABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.2\sqrt 3 .{\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = 3\]

Vậy\[\min {V_{S.ABC}} = 3\]

Đáp án cần chọn là: A