Khối chóp có đáy là hình bình hành, một cạnh đáy bằng a và các cạnh bên đều bằng

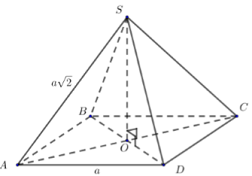
Gọi \[O = AC \cap BD\]

Tam giác SAC cân tại S, SO là trung tuyến\[ \Rightarrow SO \bot AC\]

Tam giác SBD cân tại S, SO là trung tuyến \[ \Rightarrow SO \bot BD\]

\[ \Rightarrow SO \bot \left( {ABCD} \right)\]

Vì \[SA = SB = SC = SDSO \bot \left( {ABCD} \right)\] nên O là tâm đường tròn ngoại tiếp ABCD.

Hình bình hành ABCD nội tiếp đường tròn (O) nên ABCD phải là hình chữ nhật.

Theo bài ra ta giả sử AD=a và đặt\[AB = x\,\,\left( {x > 0} \right)\]

Áp dụng định lí Pytago trong tam giác vuông ABC có:

\[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {x^2}} \]

\[ \Rightarrow AO = \frac{1}{2}AC = \frac{1}{2}\sqrt {{a^2} + {x^2}} \]

Áp dụng định lí Pytago trong tam giác vuông SOA có:

\[SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {2{a^2} - \frac{{{a^2} + {x^2}}}{4}} = \frac{1}{2}\sqrt {7{a^2} - {x^2}} \]

Khi đó ta có

\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{1}{2}\sqrt {7{a^2} - {x^2}} .ax = \frac{a}{6}x\sqrt {7{a^2} - {x^2}} \]

Áp dụng BĐT Cô-si ta có:\[x\sqrt {7{a^2} - {x^2}} \le \frac{{{x^2} + 7{a^2} - {x^2}}}{2} = \frac{{7{a^2}}}{2}\]

\[ \Rightarrow {V_{S.ABCD}} \le \frac{a}{6}.\frac{{7{a^2}}}{2} = \frac{{7{a^3}}}{{12}}\]

Dấu “=” xảy ra \[ \Leftrightarrow {x^2} = 7{a^2} - {x^2} \Leftrightarrow x = \frac{{a\sqrt {14} }}{2}\]

Vậy thể tích khối chóp S.ABCD đạt giá trị lớn nhất bằng\[\frac{{7{a^3}}}{{12}} \Leftrightarrow x = \frac{{a\sqrt {14} }}{2}\]