Cho hình trụ bán kính đường tròn đáy bằng 1. Hai điểm A và B lần lượt thuộc hai đường tròn đáy sao cho

* Hướng dẫn giải

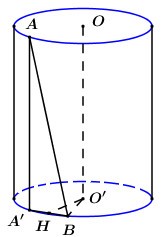
Gọi O,O′ lần lượt là tâm đường tròn đáy chứa A,B.

Gọi A′ là hình chiếu của A lên đường tròn đáy chứa điểm B.

Ta có\[AA'\parallel OO' \Rightarrow OO'\parallel \left( {AA'B} \right) \supset AB\]

\[ \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\]

Gọi H là trung điểm của A′B, ta có \[O'H \bot A'B\] (quan hệ vuông góc giữa đường kính và dây cung).

Khi đó ta có:\(\left\{ {\begin{array}{*{20}{c}}{O\prime H \bot A\prime B}\\{O\prime H \bot AA\prime }\end{array}} \right. \Rightarrow O\prime H \bot (AA\prime B) \Rightarrow d\left( {OO';AB} \right) = OH = \frac{1}{2}\)

Áp dụng định lí Pytago trong tam giác vuông O′HB có

\[HB = \sqrt {O'{B^2} - O'{H^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\]

\[ \Rightarrow A'B = 2HB = \sqrt 3 \]

Áp dụng định lí Pytago trong tam giác vuông  có:

\[AA' = \sqrt {A{B^2} - A'{B^2}} = \sqrt {6 - 3} = \sqrt 3 \]

Vậy thể tích khối trụ là \[V = \pi {r^2}h = \pi {.1^2}.\sqrt 3 = \pi \sqrt 3 \]Đáp án cần chọn là: C