Một hình trụ có diện tích xung quanh là

* Hướng dẫn giải

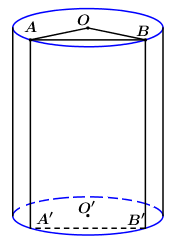
Gọi r,h lần lượt là bán kính đáy và chiều cao của hình trụ, ta có

\[{S_{xq}} = 2\pi rh \Leftrightarrow 16\pi = 2\pi rh \Leftrightarrow rh = 8\]

Lại có thiết diện qua trục là hình vuông nên \[h = 2r\]do đó \[r.2r = 8 \Leftrightarrow {r^2} = 4\]

\[ \Rightarrow r = 2,\,\,h = 4 = AA'\]

Theo bài ra ta có: \[\angle AOB = {120^0}\]Áp dụng định lí Cosin trong tam giác OAB ta có:

\[\begin{array}{*{20}{l}}{A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB}\\{A{B^2} = {r^2} + {r^2} - 2.r.r.\cos {{120}^0}}\\{A{B^2} = 3{r^2}}\\{ \Rightarrow AB = r\sqrt 3 = 2.\sqrt 3 }\end{array}\]

Vậy \[{C_{ABB'A'}} = 2\left( {AB + AA'} \right) = 2\left( {2\sqrt 3 + 4} \right) = 8 + 4\sqrt 3 \]Đáp án cần chọn là: D