Cho khối trụ có hai đáy là (O) và (O′). AB,CD lần lượt là hai đường kính của (O) và (O′), góc giữa AB và CD bằng 300, AB = 6 và thể tích khối tứ diện ABCD bằng 30. Thể tích khối tr...

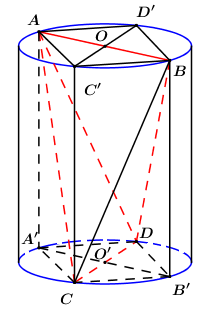
Gọi A′,B′ lần lượt là hình chiếu của A,B lên đường tròn (O).

      C′,D′ lần lượt là hình chiếu của C,D lên đường tròn (O′).

=>AC′BD′ là hình bình hành, lại có AB = CD = C′D′ nên  AC′BD′ là hình chữ nhật.

Khi đó AC′BD′.A′CB′D là hình hộp chữ nhật.

Ta có:\[{V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\]

Ta có:\[{V_{A.A'CD}} = \frac{1}{3}AA'.{S_{A'CD}} = \frac{1}{3}AA'.\frac{1}{2}{S_{A'CB'D}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]

CMTT ta có: \[{V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]

\[\begin{array}{*{20}{l}}{ \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\frac{1}{6}{V_{AC'BD'.A'CB'D}}}\\{ \Rightarrow {V_{ABCD}} = \frac{1}{3}{V_{AC'BD'.A'CB'D}} = 30}\\{ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90}\end{array}\]

Theo bài ra ta có: \[\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\]giả sử\[\angle \left( {AB;C'D'} \right) = \angle \[ \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\]Lại có  \[OA = OC' = \frac{1}{2}AB = 3\]

\[ \Rightarrow {S_{OAC'}} = \frac{1}{2}OA.OC'.\sin \angle AOC' = \frac{1}{2}.3.3.\sin {30^0} = \frac{9}{4}\]

Ta có:  \[{V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}} \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\]

Vậy thể tích khối trụ là  \[V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \]