Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính

* Hướng dẫn giải

Gọi độ dài đường cao của ống trụ là 10x(cm)(x > 0)

Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là x(cm).

Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là x và \[2\pi .R = 2\pi .\frac{2}{\pi } = 4\,\,\left( {cm} \right)\]

Khi đó độ dài đường chéo của hình chữ nhật là \[\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \], và độ dài đường chéo chính bằng độ dài của 1 vòng.

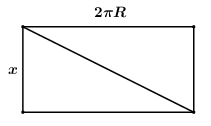
Do đó ta có phương trình:  \[10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\]

\[ \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\]Độ dài đường cao của ống trụ là \[h = 10x = 30(cm)\]

Vậy diện tích xung quanh của ống trụ là \[{S_{xq}} = 2\pi Rh = 2\pi .\frac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\].

Đáp án cần chọn là: D