Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng

* Hướng dẫn giải

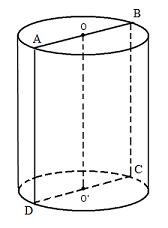
Gọi R,h lần lượt là bán kính đáy và chiều cao của hình trụ.

Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật ABCD như hình vẽ, ta có AB = 2R và AD = h.

Chu vi thiết diện chứa trục bằng 12 \[ \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\]

Khi đó thể tích khối trụ:

\[V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right) \le \pi .{\left( {\frac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \]

Dấu “=” xảy ra khi và chỉ khi \[R = 6 - 2R \Leftrightarrow R = 2.\]

Vậy thể tích khối trụ lớn nhất là \[8\pi \] khi R = 2.

Đáp án cần chọn là: C