Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng
Câu hỏi :
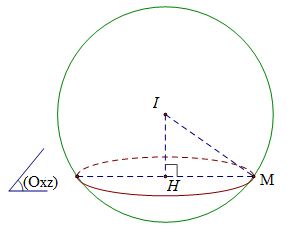
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng \[\Delta :\frac{x}{1} = \frac{{y + 3}}{1} = \frac{z}{2}\;\]. Biết rằng mặt cầu (S) có bán kính bằng \(2\sqrt 2 \)và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.
A.I(1;−2;2),I(5;2;10)
B.I(1;−2;2),I(0;3;0)
C.I(5;2;10),I(0;−3;0)
D.I(1;−2;2),I(−1;2;−2)
* Đáp án
* Hướng dẫn giải
Tâm I thuộc đường thẳng d nên\[I\left( {t; - 3 + t;2t} \right)\]
Phương trình mặt phẳng\[\left( {{\rm{Oxz}}} \right):y = 0\]
Ta có bán kính mặt cầu \[IM = 2\sqrt 2 \], mặt cầu cắt mặt phẳng (Oxz) theo đường tròn có bán kính HM=2 suy ra\[d\left( {I,\left( {Oxz} \right)} \right) = IH = \sqrt {I{M^2} - H{M^2}} = \sqrt {8 - 4} = 2\]
Ta có\[\left| { - 3 + t} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3 + t = 2}\\{ - 3 + t = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 5 \Rightarrow I(5;2;10)}\\{t = 1 \Rightarrow I(1; - 2;2)}\end{array}} \right.\]
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Các bài toán về đường thẳng và mặt cầu !!
Copyright © 2021 HOCTAP247
