Cho tứ diện ABCD có G là điểm thỏa mãn vecto GA + vecto GB + voecto GC + vecto GD = 0. Mặt phẳng thay đổi chứa BG
Câu hỏi :
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Gọi O là trọng tâm tam giác BCD
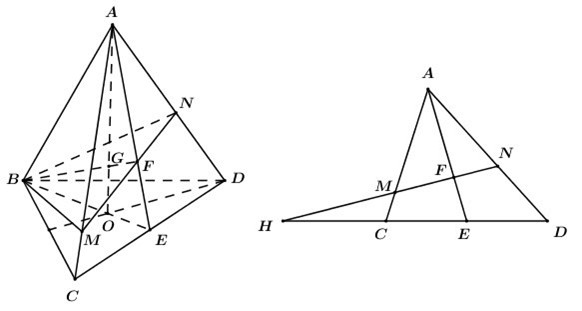
Trong (ABE) gọi
Lấy trong (ACD) gọi khi đó ta có mặt phẳng chứa BG cắt AC,AD lần lượt tại M,N chính là (BMN).
Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:
là trọng tâm tam giác ACD.
Trong (ACD) kéo dài MN cắt CD tại H. Đặt
Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:
Ta có:
Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:
Khi đó ta có
Xét hàm số ta có
BBT:
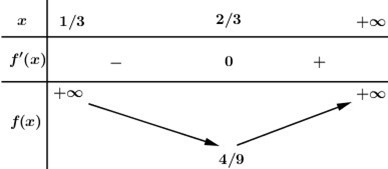
Dựa vào BBT ta thấy
Vậy giá trị nhỏ nhất của tỉ số
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Thể tích khối chóp !!
Số câu hỏi: 37
Copyright © 2021 HOCTAP247
