Thể tích khối chóp !!
Câu 1 :
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
A.
B.
C.
D.
Câu 2 :
Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:
A.
B.
C.
D.
Câu 3 :
Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
A.
B.
C.
D.
Câu 4 :
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
A.
B.
B.
C.
Câu 5 :
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn và . Thể tích khối chóp S.BCD là:
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn và . Thể tích khối chóp S.BCD là:
A.
B.
C.
D.
Câu 6 :
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
A.
B.
C.
D.
Câu 7 :
Cho hình chóp đều S.ABCD có diện tích đáy là , diện tích một mặt bên là . Thể tích khối chóp S.ABCD là:
Cho hình chóp đều S.ABCD có diện tích đáy là , diện tích một mặt bên là . Thể tích khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 8 :
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 600. Thể tích khối chóp S.ABC là:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 600. Thể tích khối chóp S.ABC là:
A.
B.
C.
D.
Câu 9 :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,BC=2AB=2a. Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng 600. Thể tích khối chóp đó bằng:
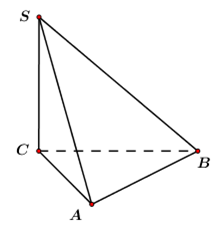
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,BC=2AB=2a. Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng 600. Thể tích khối chóp đó bằng:

A.
B.
C.
D.
Câu 10 :
Cho khối chóp S.ABCD có thể tích bằng , đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng . Tính khoảng cách từ M tới mặt phẳng (SAB).
Cho khối chóp S.ABCD có thể tích bằng , đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng . Tính khoảng cách từ M tới mặt phẳng (SAB).
A.12a
B.6a
C.3a
Câu 11 :
Cho hình chóp S.ABCD có . Biết , cạnh SC tạo với đáy một góc 600 và diện tích tứ giác ABCD là . Gọi H là hình chiếu của A trên cạnh SC. Tính thể tích khối chóp H.ABCD.
A.
B.
C.
D.
Câu 12 :
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết , SC hợp với (SAB) một góc 300 và (SAC) hợp với đáy (ABC) một góc 600. Thể tích khối chóp là:
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết , SC hợp với (SAB) một góc 300 và (SAC) hợp với đáy (ABC) một góc 600. Thể tích khối chóp là:
A.
B.
C.
D.
Câu 13 :
Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau, . Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CD,DB. Thể tích V của tứ diện AMNP là:
Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau, . Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CD,DB. Thể tích V của tứ diện AMNP là:
A.
B.
C.
D.
Câu 15 :
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Gọi M là trung điểm của . Thể tích khối chóp là:
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Gọi M là trung điểm của . Thể tích khối chóp là:
A.
B.
C.
D.
Câu 16 :
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 600. Thể tích hình chóp là:
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 600. Thể tích hình chóp là:
A.
B.
C.
D.
Câu 17 :
Thể tích khối bát diện đều cạnh a bằng:
Thể tích khối bát diện đều cạnh a bằng:
A.
B.
C.
D.
Câu 18 :
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
A.
B.
C.
D.
Câu 19 :
Cho hình chóp S.ABC có . Tính thể tích khối chóp S.ABC.
Cho hình chóp S.ABC có . Tính thể tích khối chóp S.ABC.
A.
B.
C.
D.
Câu 21 :
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 600. Thể tích của khối chóp đó là:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 600. Thể tích của khối chóp đó là:
A.16
B.
C.
D.
Câu 22 :
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là có thể tích lớn nhất bằng
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là có thể tích lớn nhất bằng
A.
B.
C.
D.
Câu 23 :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho . Thể tích khối tứ diện MNEF bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho . Thể tích khối tứ diện MNEF bằng
A.
B.
C.
D.
Câu 24 :
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, M là trung điểm của AB, tam giác SMC vuông tại tạo với đáy góc 600. Thể tích của khối chóp S.ABCD là:
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, M là trung điểm của AB, tam giác SMC vuông tại tạo với đáy góc 600. Thể tích của khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 26 :
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng . Thể tích khối chóp S.ABCD là:
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng . Thể tích khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 28 :
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là
A.
B.
C.
D.
Câu 30 :
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và có thể tích . Tìm số r>0 sao cho tồn tại điểm J nằm trong khối chóp mà khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r?
A.
B.
C.
D.
Câu 32 :
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng . Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng . Tính thể tích nhỏ nhất của khối chóp S.ABC
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng . Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng . Tính thể tích nhỏ nhất của khối chóp S.ABC
A. 3
B.
C.
D. 4
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
