Cho tứ diện ABCD có AB=a căn bậc hai của 6, tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD)
Câu hỏi :
Cho tứ diện ABCD có , tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD) trùng với trực tâm H của tam giác BCD, mặt phẳng (ADH) tạo với mặt phẳng (ACD) một góc 450. Tính thể tích khối tứ diện ABCD.
Cho tứ diện ABCD có , tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD) trùng với trực tâm H của tam giác BCD, mặt phẳng (ADH) tạo với mặt phẳng (ACD) một góc 450. Tính thể tích khối tứ diện ABCD.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
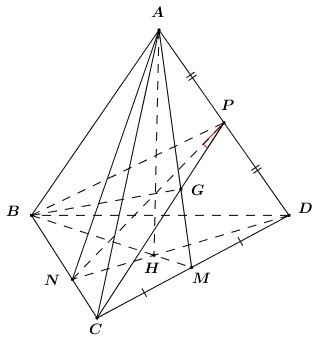
Gọi BM,DN lần lượt là các đường cao của tam giác
Ta có:
⇒AM là đường cao của tam giác đều ACD, do đó M là trung điểm của CD.
Gọi P là trung điểm của AD, do đều nên
Ta có:
Ta có:
Ta có: vuông tại N, lại có
hay
Gọi là trọng tâm tam giác đều ACD.
Ta có:
mà G là trọng tâm tam giác đều
Ta có vuông tại G (2).
Từ (1) và (2) suy ra tam giác BCG vuông cân tại
Ta có: đều cạnh 3a3a nên
Vậy
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Thể tích khối chóp !!
Số câu hỏi: 37
Copyright © 2021 HOCTAP247
