Sơ đồ mạch điện có dạng như hình vẽ, điện trở R = 40W, cuộn thuần cảm (L=frac{3}{10pi }(H))
Câu hỏi :
Sơ đồ mạch điện có dạng như hình vẽ, điện trở R = 40W, cuộn thuần cảm \(L=\frac{3}{10\pi }(H)\) , tụ điện \(C=\frac{10^{-3}}{7\pi }(F)\) . Điện áp \(u_{AF}=120cos(100\pi t)\) (V).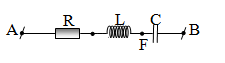
A. \(i=2,4cos(100\pi t-\frac{37\pi }{180})(A)\)
B. \(i=2,4cos(100\pi t-\frac{3\pi }{180})(A)\)
C. \(i=2cos(100\pi t-\frac{37\pi }{180})(A)\)
D. \(i=2,4cos(200\pi t-\frac{37\pi }{180})(A)\)
* Đáp án
A
* Hướng dẫn giải
Cảm kháng:
\(Z_L=\omega L=100\pi.\frac{3}{10\pi }=30\Omega\)
Dung kháng:
\(Z_C=\frac{1}{\omega C}=\frac{1}{100\pi.\frac{10^{-3}}{7\pi }}=70\Omega\)
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\
= \sqrt {{R^2} + {Z_L}2} \\
= \sqrt {{{40}^2} + {{30}^2}} = 50\Omega
\end{array}\)
Suy ra:
\(\begin{array}{l} {I_0} = \frac{{{U_{AF}}}}{{{Z_{AF}}}} = \frac{{120}}{{50}} = 2,4(A)\\ tan{\varphi _{AF}} = \frac{{{Z_L}}}{R} = \frac{{20}}{{40}} = 0,75\\ \Rightarrow {\varphi _{AF}} = \frac{{37\pi }}{{180}}(rad)\\ {\varphi _u} = {\varphi _i} + {\varphi _{AF}} = 0\\ \to {\varphi _i} = - \frac{{37\pi }}{{180}}(rad) \end{array}\)
Vậy, \(i=2,4cos(100\pi t-\frac{37\pi }{180})(A)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Vật lý 12 Bài 14 Mạch có R, L, C mắc nối tiếp
Copyright © 2021 HOCTAP247
