Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
30 Bài tập trắc nghiệm Vật lý 12 chương Sóng cơ và sóng âm nâng cao
Trên mặt nước, tại hai điểm A và B cách...
Trên mặt nước, tại hai điểm A và B cách nhau 44 cm có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai són
Câu hỏi :
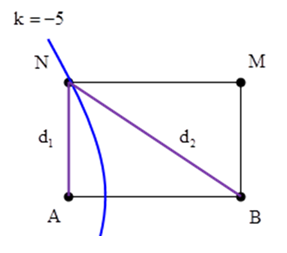
Trên mặt nước, tại hai điểm A và B cách nhau 44 cm có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai sóng kết hợp có bước sóng 8 cm. Gọi M và N là hai điểm trên mặt nước sao cho ABMN là hình chữ nhật. Để trên MN có số điểm dao động với biên độ cực đại nhiều nhất thì diện tích hình chữ nhật ABMN lớn nhất gần giá trị nào nhất sau đây?
A. 260 cm2.
B. 180 cm2.
C. 180 mm2.
D. 260 mm2.
* Đáp án
B
* Hướng dẫn giải
Số điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn
\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow - \frac{{44}}{8} < k < \frac{{44}}{8} \Leftrightarrow - 5,5 < k < 5,5\)
+ Để số điểm dao động với biên độ cực đại trên MN là nhiều nhất thì N phải nằm trên hypebol cực đại ứng với \(k = - 5\)
+ N nằm trên cực đại nên ta có
\({d_2} - {d_1} = 5\lambda = 40cm\)
Mặc khác
\({d_2} = \sqrt {{d_1} + {{44}^2}} \Rightarrow \sqrt {{d_1} + {{44}^2}} - {d_1} = 40 \Rightarrow {d_1} = 42cm\)
Diện tích của hình chữ nhật
\(S = AB.AN = 44.4,2 = 184,8c{m^2}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 Bài tập trắc nghiệm Vật lý 12 chương Sóng cơ và sóng âm nâng cao
Số câu hỏi: 29
Copyright © 2021 HOCTAP247