Điện áp xoay chiều (u = U_0 cos omega t (V)) vào hai đầu đoạn mạch AB theo thứ tự

* Hướng dẫn giải

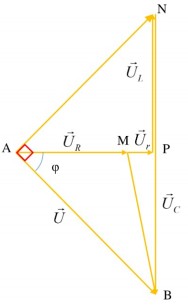
Xét tam giác \(\Delta AMB\) ta có: \(U^2_{MB}= U^2 + U^2_R - 2 UU_R cos \varphi\)

\(U_{MB}\) cực tiểu khi \(cos \varphi\) cực đại \(\rightarrow \varphi = 0\)→mạch có cộng hưởng điện

\(Z_{C1} = Z_L\) hay \(U_{C1} =U_L\)\(\rightarrow U_1 = U_{MB}= U_r = u \frac{r}{R + r} = \frac{U}{10} (1)\)

Xét tam giác \(\Delta ANB\), theo định lí hàm sin trong tam giác ta có:

\(\frac{U_c}{sin (NAB)} = \frac{U}{sin (ANB)}\)

\(\Leftrightarrow U_C = \frac{U sin (NAB)}{cos (NAM)} = \frac{Usin (NAB)}{cos \varphi _{RrL}}\)

Vì \(\varphi _{RrL}\) không đổi nên, \(U_c\) cực đại khi \(sin (NAB)= 1 \Rightarrow NAB = 90^0\)

Mặt khác khi \(C = C_2 = \frac{C_1 }{2}\rightarrow Z_{C2} = 2 Z_{C1} = 2 Z_L \rightarrow U_{C2}= 2U_L\)\(\rightarrow NB = 2 NP\) hay \(NP = PB\) → tam giác \(\Delta ANB\) vuông tại A

\(\rightarrow NB = AB\sqrt{2}\Rightarrow U_2 = U_{C2} = U\sqrt{2}(2)\)

Từ (1) và (2) suy ra: \(\frac{U_2}{U_1} = 10 \sqrt{2}\)