Tại mặt chất lỏng có hai nguồn phát sóng giống nhau A, B cách nhau một đoạn 8 cm.

* Hướng dẫn giải

Công thức tính diện tích hình thang: \(S = \frac{h (AB + MN)}{2}\)

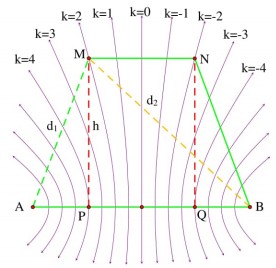
Do AMNB là hình thang cân và cạnh MN bị giới hạn sao cho chứa 5 cực đại giao thoa, nên để diện tích hình thang lớn nhất thì h phải lớn nhất → M và N phải nằm trên các vân cực đại bậc 2 như hình vẽ

Gọi P, Q là hình chiếu của M, N lên AB \(\rightarrow \Delta AMP\) và \(\Delta BMP\) là tam giác vuông

\(\rightarrow AM = \sqrt{MP^2 + AP^2} =\sqrt{h^2 + 2^2}\)

và \(BM = \sqrt{MP^2 + BP^2} = \sqrt{h^2 + 6}\)

Vì M nằm trên vân cực đại bậc 2, nên theo điều kiện cực đại giao thoa thì:

\(d_2 - d_1 = 2 \lambda \Rightarrow BM - AM = 2 \Leftrightarrow \sqrt{h^2 + 6^2} - \sqrt{h^2 + 2^2} = 2\)

\(\Leftrightarrow \sqrt{h^2 + 6^2} = 2 + \sqrt{h^2 + 2^2}\Rightarrow h^2 + 6^2 = 4 + 4\sqrt{h^2 + 2^2 } + h^2 + 2^2\)\(\Leftrightarrow \sqrt{h^2 + 2^2} = 7 \Rightarrow h = 3\sqrt{5}cm\)

\(\Leftrightarrow S = \frac{3\sqrt{5}(8+ 4)}{2}= 18\sqrt{5}cm^2\)