Trên một sợi dây OB căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định.
Câu hỏi :
Trên một sợi dây OB căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định. Gọi M, N và P là ba điểm trên dây có vị trí cân bằng cách B lần lượt 4 cm, 6 cm và 38 cm. Hình vẽ mô tả dạng sợi dây ở thời điểm t1 (đường 1) và thời điểm t2 = t1 + \(\frac{11}{12f}\)(đường 2). Tại thời điểm t1, li độ của phần tử dây ở N bằng biên độ của phần tử dây ở M và tốc độ của phần tử dây ở M là 60 cm/s . Tại thời điểm t2, vận tốc của phần tử dây ở P là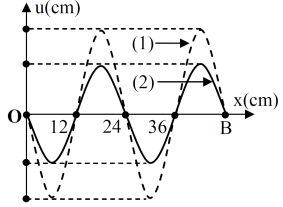
A. \(20\sqrt{3}\) cm/s
B. 60 cm/s
C. \(- 20\sqrt{3}\) cm/s
D. – 60 cm/s
* Đáp án
D
* Hướng dẫn giải
- Ta thấy: \(\lambda =24(cm)\) và gọi biên độ của điểm bụng là A.
\(MB=\frac{\lambda }{6}\Rightarrow A_M=\frac{A\sqrt{3}}{2}\)
\(NB=\frac{\lambda }{4}\Rightarrow A_N = A\)
\(PB=\lambda +\frac{\lambda }{2}+\frac{\lambda }{12}\Rightarrow A_P = \frac{A}{2}\)
- Dựa vào đồ thị:
+ M và N cùng pha nhau:
\(\Rightarrow \frac{u_M}{u_N}=\frac{A_M}{A_N}=\frac{A\frac{\sqrt{3}}{2}}{A}=\frac{\sqrt{3}}{2}\)
+ M và P ngược pha nhau:
\(\Rightarrow \frac{u_P}{u_M} = - \frac{A_P}{A_M}=-\frac{\frac{A}{2}}{\frac{A\sqrt{3}}{2}}=-\frac{1}{\sqrt{3}}\Rightarrow \frac{v_P}{v_M}=-\frac{1}{\sqrt{3}}(*)\)
- Thời điểm t1: \(u_N=A_M\Rightarrow u_M=\frac{\sqrt{3}}{2}A_M\)
\(\Rightarrow v_{1M}=\frac{v_{Mmax}}{2}\Rightarrow v_{Mmax}=2v_{1M}=120(cm/s)\)
- Thời điểm : \(t_2=t_1+\frac{11T}{12}:\)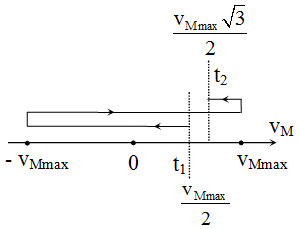
\(v_{2M}=\frac{v_{Mmax\sqrt{3}}}{2}=60\sqrt{3}(cm/s)\)
Lúc đó, từ \((*)\Rightarrow v_{2P}=-\frac{1}{\sqrt{3}}v_{2M}=-60(cm/s)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 Bài tập trắc nghiệm Vật lý 12 chương Sóng cơ và sóng âm nâng cao
Copyright © 2021 HOCTAP247
