Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
30 Bài tập trắc nghiệm Dao động điều hòa Vật lý 12 nâng cao
Khi một chất điểm M chuyển động tròn đều trên...
Khi một chất điểm M chuyển động tròn đều trên đường tròn tâm O, bán kính (R = 10cm) nằm trong mặt phẳng tọa độ
Câu hỏi :
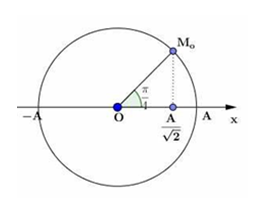
.PNG)
Khi một chất điểm M chuyển động tròn đều trên đường tròn tâm O, bán kính \(R = 10cm\) nằm trong mặt phẳng tọa độ Oxy theo chiều ngược ngược chiều kim đồng hồ với tốc độ góc \(\omega = 2\pi \left( {rad/s} \right)\) . Tại thời điểm ban đầu, bán kính OM tạo với trục Ox góc \(\varphi = \frac{\pi }{6}\) như hình vẽ. Hình chiếu của điểm M trên trục Oy có tung độ biến đổi theo thời gian với phương trình:
A. \(y = 10.\cos \left( {2\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
B. \(y = 10.\cos \left( {2\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\)
C. \(y = 10.\cos \left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)\)
D. \(y = 10.\cos \left( {2\pi t - \frac{\pi }{6}} \right)\left( {cm} \right)\)
* Đáp án
A
* Hướng dẫn giải
Hình chiếu của M lên trục Oy dao động với phương trình:
\(y = 10\sin \left( {2\pi t + \frac{\pi }{6}} \right) = 10\cos \left( {2\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 Bài tập trắc nghiệm Dao động điều hòa Vật lý 12 nâng cao
Số câu hỏi: 23
Copyright © 2021 HOCTAP247