Một con lắc lò xo nằm ngang, vật có khối lượng m = 100g
Câu hỏi :
Một con lắc lò xo nằm ngang, vật có khối lượng m = 100g chuyển động không ma sát dọc theo trục của một lò xo cứng k = 25 N/m. Khi vật đang đứng yên tại vị trí lò xo không biến dạng thì bắt đầu tác dụng lực F có hướng và độ lớn không thay đổi, bằng 1 N lên vật như hình vẽ. Sau khoảng thời gian ∆t thì ngừng tác dụng lực. Biết rằng sau đó vật dao động với tốc độ cực đại bằng 20√30 cm/s. Nếu tăng gấp đôi thời gian tác dụng lực thì vận tốc cực đại sau khi ngừng tác dụng lực là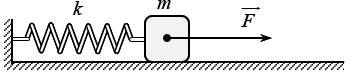
A. 60 √10 cm/s.
B. 20 √30 cm/s.
C. 40 √15 cm/s.
D. 40 √30 cm/s.
* Đáp án
B
* Hướng dẫn giải
Ta có:
- \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{\left( {25} \right)}}{{\left( {{{100.10}^{ - 3}}} \right)}}} = 5\sqrt {10} (rad/s)\)
- \(\Delta {l_0} = \frac{F}{k} = \frac{{\left( 1 \right)}}{{\left( {25} \right)}} = 4cm\)
Dưới tác dụng của lực F con lắc sẽ dao động điều hòa quanh vị trí cân bằng mới A', với biên độ A' =4 cm.
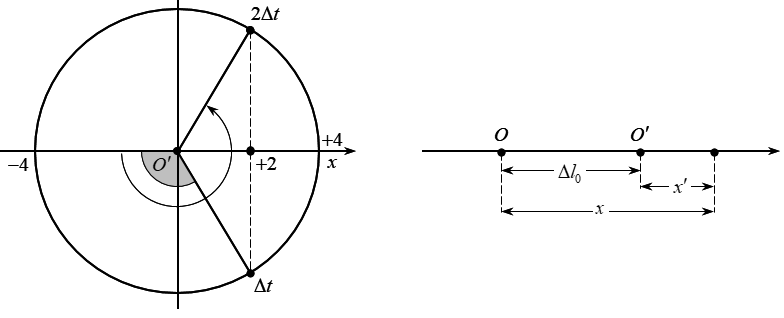
Giả sử, sau khoảng thời gian ∆t vật đến vị trí cách vị trí lò xo không biến dạng (O) một đoạn . Lúc này:
- li độ của vật so với vị trí cân bằng mới \(x' = \Delta {l_0} + x = x - 4\).
- vận tốc của vật \({v^2} = {\omega ^2}\left[ {{A^2} - {{\left( {x'} \right)}^2}} \right] = {\omega ^2}\left[ {{4^2} - {{\left( {x - 4} \right)}^2}} \right]\)
Ngừng tác dụng của lực thì con lắc lại dao động quanh vị trí lò xo không biến dạng với biên độ A', trong đó:
- \({v_{max}} = \omega A' \to A' = \frac{{{v_{max}}}}{\omega } = \frac{{\left( {20\sqrt {30} } \right)}}{{\left( {5\sqrt {10} } \right)}} = 4\sqrt 3 \) cm.
- \(\begin{array}{l}
{{A'}^2} = {x^2} + \left[ {{4^2} - {{\left( {x - 4} \right)}^2}} \right] \to {v_{max}} = \omega A' \to A' = \frac{{{v_{max}}}}{\omega } = \frac{{\left( {20\sqrt {30} } \right)}}{{\left( {5\sqrt {10} } \right)}} = 4\sqrt 3 \\
\Rightarrow {\left( {4\sqrt 3 } \right)^2} = {x^2} + \left[ {{4^2} - {{\left( {x - 4} \right)}^2}} \right] \Rightarrow x = 6cm
\end{array}\)
→ So với vị trí cân bằng mới vật đi đến vị trí x' = 2 cm thì ngừng lực tác dụng → khoảng thời gian tương ứng là:
\(\Delta t = \frac{T}{4} + \frac{T}{{12}} = \frac{T}{3}\)
→ Tăng gấp đôi thời gian \(\Delta t' = \Delta t = \frac{{2T}}{3}\), lúc này vật đi qua vị trí x'=2 cm nhưng theo chiều âm, kết quả là khi ngừng lực tác dụng thì tốc độ cực đại sau đó của con lắc vẫn là \({v_{max}} = 20\sqrt {30} \) cm/s.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Hưng Phú
Copyright © 2021 HOCTAP247