Đặt điện áp (ω không đổi)

* Hướng dẫn giải

Ta có:

• R, L không đổi → φ_RL là hằng số → ∆φ_{RL_C} cũng là hằng số.
•  \(\overrightarrow {{U_{AB}}}  = \overrightarrow {{U_{RL}}}  + \overrightarrow {{U_C}} \)→ M có quỹ tích là đường tròn.
•  \({\varphi _{RL}} = arctan\left( {\frac{{{Z_L}}}{R}} \right) = arctan\left( {\sqrt 3 } \right) = {60^0}\)→ \(\alpha  = {30^0}\).

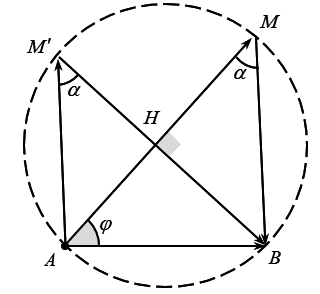
Từ giản đồ vecto

• C = C₁ thì U_Cmax → AM là đường kính của đường tròn và góc ABM là góc vuông.

\(\varphi  = arc\cos \left( {\frac{{AB}}{{AM}}} \right) = arc\cos \left( {\frac{{50}}{{100}}} \right) = {60^0}\)

→ \(HB = AB\sin \varphi  = \left( {50} \right)\sin \left( {60} \right) = 25\sqrt 3 \)V và \(AH = AB\cos \varphi  = \left( {50} \right)\cos \left( {{{60}^0}} \right) = 25\)V.

• ∆AM’H vuông tại H → \(M'H = \frac{{AH}}{{\tan \alpha }} = \frac{{\left( {25} \right)}}{{\tan \left( {{{30}^0}} \right)}} = 25\sqrt 3 \)V.

→ \({U_0} = HB + AM' = \left( {25\sqrt 3 } \right) + \left( {25\sqrt 3 } \right) \approx 87\)V.