Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Cơ
Một người chạy tập thể dục
Một người chạy tập thể dục
Câu hỏi :
Một người chạy tập thể dục trên một con đường hình vuông khép kín có chu kì 400 m. Bên trong vùng đất được bao bởi con đường có đặt một nguồn âm điểm phát âm đẳng hướng ra bên ngoài. Khi đi hết một vòng khép kín thì người đó thấy có hai vị trí mà mức cường độ âm bằng nhau và là lớn nhất có giá trị L1 và có một điểm duy nhất mức cường độ âm nhỏ nhất là L2 trong đó L1=L2+10 dB. Khoảng cách từ nguồn âm đến tâm của hình vuông tạo bởi con đường gần nhất với giá trị nào sau đây?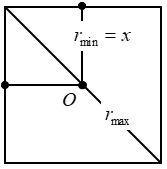
A. 40 m
B. 31 m
C. 36 m
D. 26 m
* Đáp án
D
* Hướng dẫn giải
Để tồn tại duy nhất một điểm có cường độ âm nhỏ nhất thì nguồn âm phải nằm trên đường chéo của hình vuông.
\(\begin{array}{l} \frac{{{r_{max}}}}{{{r_{\min }}}} = {10^{\frac{{\Delta L}}{{20}}}} = \sqrt {10} \\ x = {r_{\min }} \Rightarrow \sqrt {10} x + \sqrt 2 x = 100\sqrt 2 \Rightarrow x \approx 31cm \end{array}\)
Khoảng cách từ nguồn âm O đến tâm hình vuông là \(d = 50\sqrt 2 - 31\sqrt 2 \approx 27m\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Cơ
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
