Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Lạc
Một con lắc lò xo treo thẳng đứng được kích...
Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa
Câu hỏi :
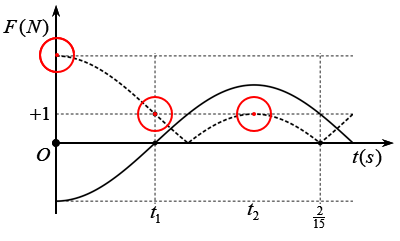
Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa với biên độ A. Một phần đồ thị biểu diễn sự phụ thuộc thời gian của lực phục hồi và độ lớn của lực đàn hồi tác dụng vào con lắc trong quá trình dao động được cho như hình vẽ. Lấy g=10=π2 m/s2. Độ cứng của lò xo là
A. 100 N/m
B. 400 N/m
C. 300 N/m
D. 200 N/m
* Đáp án
A
* Hướng dẫn giải
Ta có:
- \({F_{ph}} = - kx\)→ biểu diễn bằng đường nét liền.
- \({F_{dh}} = k\left| {\Delta {l_0} + x} \right|\)→ biểu diễn bằng đường nét đứt.
Từ đồ thị:
- t1: \(\left\{ \begin{array}{l}
{F_{dh}} = 1\\
{F_{ph}} = 0
\end{array} \right.\)→ vật đi qua vị trí cân bằng, lò xo đãn giãn một đoạn \(\Delta {l_0}\)→ \(k\Delta {l_0} = 1\) (1). - t2: \({F_{dh}} = 1\), trong khoảng thời gian từ t1 đến t2 vật đi qua vị trí \({F_{dh}} = 0\)→ tương ứng với trường hợp vật ở biên trên → \({F_{dh}} = k\left( {A - \Delta {l_0}} \right)\)(2).
Từ (1) và (2) → \(A = 2\Delta {l_0}\).
- t=0: \({F_{dh}} = {F_{dhmax}}\)→ vật ở biên dưới; t=2/5s vật đi qua vị trí lò xo không biến dạng lần thứ 2.
→ \(\Delta t = t - {t_0} = \frac{{2T}}{3} = \frac{2}{{15}}\)s → T=0,2s → \(\Delta {l_0} = 1\)cm.
→ \(k = \frac{{{{\left( {{F_{dh}}} \right)}_{{t_2}}}}}{{\Delta {l_0}}} = \frac{{\left( 1 \right)}}{{\left( {{{1.10}^{ - 2}}} \right)}} = 100\)N/m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Lạc
Số câu hỏi: 40
Copyright © 2021 HOCTAP247