Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Lạc
Ở mặt chất lỏng, tại hai điểm A và B
Ở mặt chất lỏng, tại hai điểm A và B
Câu hỏi :
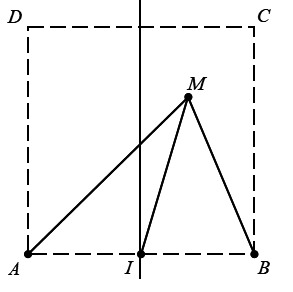
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra sóng kết hợp với bước sóng λ. Gọi C và D là hai điểm trên mặt chất lỏng sao cho ABCD là hình vuông, I là trung điểm của AB, M là một điểm trong hình vuông ABCD xa I nhất mà phần tử chất lỏng tại đó dao động với biên độ cực đại và cùng pha với nguồn. Biết AB=6,6λ. Độ dài đoạn thẳng MI gần nhất giá trị nào sau đây?
A. 6,17λ
B. 6,25λ
C. 6,49λ
D. 6,75λ
* Đáp án
B
* Hướng dẫn giải
Để đơn giản, ta chọn λ=1. Ta có:
- \(\left\{ \begin{array}{l}
AM + BM = n\\
AM - BM = k
\end{array} \right.\) (1) điều kiện để M cực đại cùng pha, n và k cùng tính chất chẵn lẻ. - vì tính đối xứng ta chỉ xét điểm M thuộc các cực đại k>0.
AB/λ = 6,6 →k = 0,1,…,6.
- \(\frac{{{{\left( {AM + BM} \right)}_{M \equiv C}}}}{\lambda } = \frac{{\left( {6,6\sqrt 2 } \right) + \left( {6,6} \right)}}{1} = 15,9\)→ nmax=15 và \(I{M_{max}} = \sqrt {{{\left( {6,6} \right)}^2} + {{\left( {3,3} \right)}^2}} = 7,37\)(M nằm trong hình vuông).
Mặc khác:
- \(\frac{{{{\left( {AM - BM} \right)}_{M \equiv C}}}}{\lambda } = \frac{{\left( {6,6\sqrt 2 } \right) - \left( {6,6} \right)}}{1} = 2,73\)→ để IM là lớn nhất thì M sẽ nằm trên các cực đại ứng với k=0,1,2.
MI là đường trung truyến trong tam giác ABM nên ta luôn có
\(MI = \sqrt {\frac{{A{M^2} + B{M^2}}}{2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} \)
→ Lập bảng
|
n |
k |
AM |
BM |
IM |
|
0 |
14 |
7 |
7 |
6,17 |
|
1 |
15 |
8 |
7 |
6,75 |
|
2 |
14 |
8 |
6 |
6,25 |
Chú ý: Với trường hợp k=1, dễ dàng thấy rằng M nằm ngoài hình vuông.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Âu Lạc
Số câu hỏi: 40
Copyright © 2021 HOCTAP247