Phương trình sóng tại hai nguồn A; B
Câu hỏi :
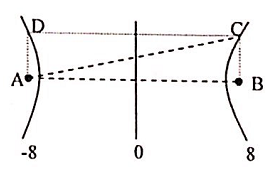
Phương trình sóng tại hai nguồn A; B là: u = 20cos(20πt) cm, cách nhau 10 cm, vận tốc truyền sóng trên mặt nước là 12 cm/s. Hai điểm C và D nằm trên hai vân cực đại và tạo với AB một hình chữ nhật ABCD có diện tích nhỏ nhất gần nhất với giá trị:
A. 8,2cm2.
B. 17,5cm2.
C. 4,1 cm2.
D. 10,6cm2.
* Đáp án
C
* Hướng dẫn giải
Bước sóng:
\(\lambda = \frac{v}{f} = \frac{{12}}{{10}} = 1,2\left( {cm} \right)\)
+ Diện tích nhỏ nhất khi C và D gần AB nhất:
+ Vậy C và D phải thuộc hai cực đại ngoài cùng của AB
+ Số cực đại trên AB được xác định bởi:
\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow - 8,3 < k < 8,3\)
=> C thuộc cực đại kC = 8 và D thuộc cực đại kD = -8
+ Vì ΔABC vuông tại C nên:
\(\begin{array}{l}
CA = \sqrt {A{B^2} + C{B^2}} \\
\Rightarrow \sqrt {A{B^2} + C{B^2}} - CB = 9,6 \Leftrightarrow \sqrt {{{10}^2} + C{B^2}} - CB = 9,6 \Rightarrow CB = 0,41\left( {cm} \right)
\end{array}\)
+ Vậy diện tích hình chữ nhật ABCD nhỏ nhất là: SABCD = AB.CB = 4,1 (cm2)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Thanh Bình
Copyright © 2021 HOCTAP247
