Hai nguồn kết hợp A, B cùng pha, cùng biên độ, cách nhau 40 cm.
Câu hỏi :
Hai nguồn kết hợp A, B cùng pha, cùng biên độ, cách nhau 40 cm. Khoảng cách giữa hai điểm dao động với biên độ cực đại gần nhau nhất trên đoạn AB là 0,8 cm. Điểm M thuộc miền giao thoa cách nguồn A một đoạn 25cm và cách nguồn B một đoạn 22cm. Dịch chuyển nguồn B từ từ dọc theo phương AB ra xa nguồn B đoạn 10cm thì điểm M chuyển thành điểm dao động với biên độ cực đại.
A. 6 lần
B. 8 lần
C. 7 lần
D. 5 lần
* Đáp án
D
* Hướng dẫn giải
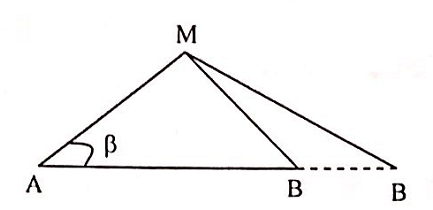
Ta có: \(\frac{\lambda }{2} = 0,8 \Rightarrow \lambda = 1,6\) (cm)
+ Từ hình có:
\(\cos \beta = \frac{{A{M^2} + {{\left( {A{B_1}} \right)}^2} - M{B_1}}}{{2AM.A{B_1}}} = 0,8705\)
+ Định lí hàm cos cho tam giác AMB2, ta có:
\(M{B_2} = \sqrt {A{M^2} = {{\left( {A{B_2}} \right)}^2} - 2AM.A{B_2}\cos \beta } = 30,8\) (cm)
+ Điểm M thuộc cực đại khi: d1M – d2M = kλ = 1,6k
+ Mặt khác có:
\(\left\{ \begin{array}{l}
\Delta {d_{M - 1}} = 25 - 22 = 3\left( {{\rm{cm}}} \right)\\
\Delta {d_{M - 2}} = 25 - 30,8 = - 5,8\left( {{\rm{cm}}} \right)
\end{array} \right. \Rightarrow - 5,8 \le 1,6k \le 3 \Rightarrow - 3,6 \le k \le 1,8\)
+ Có 5 giá trị của k nên M chuyển thành cực đại 5 lần
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Nguyễn Thị Thập
Copyright © 2021 HOCTAP247
