Con lắc lò xo có độ cứng k = 10 N/m và vật khối lượng m = 100 g
Câu hỏi :
Con lắc lò xo có độ cứng k = 10 N/m và vật khối lượng m = 100 g đặt trên phương nằm ngang. Vật có khối lượng m0 = 300 g được tích điện q = 10-4 C gắn cách điện với vật m, vật m0 sẽ bong ra nếu lực kéo tác dụng lên nó đạt giá trị 0,5 N. Đặt điện trường đều E dọc theo phương lò xo và có chiều hướng từ điểm gắn cố định của lò xo đến vật. Đưa hệ vật đến vị trí sao cho lò xo nén một đoạn 10 cm rồi buông nhẹ cho hệ vật dao động. Bỏ qua ma sát. Sau thời gian 2π/15 (s) kể từ khi buông tay thì vật m0 bong ra khỏi vật m. Điện trường E có độ lớn gần nhất với giá trị nào sau đây:
A. 909 V/m
B. 666 V/m
C. 714 V/m
D. 3333 V/m
* Đáp án
A
* Hướng dẫn giải
+ Gắn con lắc trong hệ quy chiếu của vật m, theo phương ngang vật m0 chịu tác dụng của 2 lực:
· Lực quán tính F=-ma ngược chiều với gia tốc a
· Lực điện trường F=qE cùng chiều với điện trường E
+ Chu kì dao động của hệ vật là: \(T = 2\pi \sqrt {\frac{{m + {m_0}}}{k}} = \frac{{2\pi }}{5}\) (s)
+ Chọn trục tọa độ Ox có phương nằm ngang, gốc tọa độ O là VTCB, chiều dương hướng sang phải.
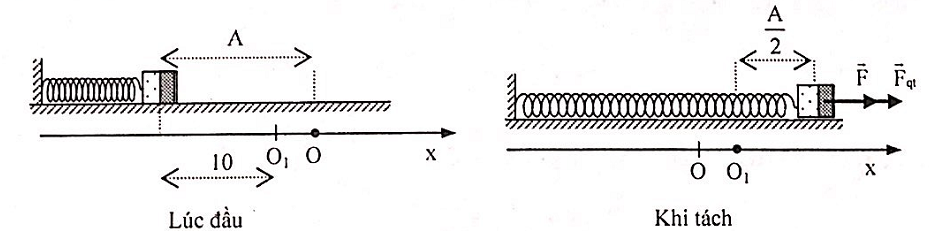
+ Khi có thêm lực điện trường tác dụng hướng sang phải thì VCTB dịch chuyển về phía phải đoạn \({x_0} = \frac{F}{k} = \frac{{\left| q \right|E}}{k}\) (so với vị trí lò xo không biến dạng). Do đó biên độ của vật là: \(A = 0,1 + \frac{{\left| q \right|E}}{k}\) (1)
+ Khi thả vật đang ở biên âm, sau thời gian: \(\Delta t = \frac{{2\pi }}{{15}} = \frac{T}{3} = \frac{T}{4} + \frac{T}{{12}}\) thì vật m0 bong nên vật m0 tách khỏi m tại vị trí x=A/2. Lúc này lực quán tính đang hướng sang phải nên hợp lực tác dụng lên vật là:
\({F_{hl}} = {F_{qt}} + F = {m_0}a + \left| q \right|E = {m_0}{\omega ^2}x + \left| q \right|E = {m_0}\left( {\frac{k}{{m + {m_0}}}} \right)\frac{A}{2} + \left| q \right|E\)
+ Theo đề, khi vật m0 bị tách thì: \({F_{hl}} = 0,5\left( N \right) \Leftrightarrow {m_0}\left( {\frac{k}{{m + {m_0}}}} \right)\frac{A}{2} + \left| q \right|E = 0,5\) (2)
+ Thay (1) vào (2), ta có:
\(\begin{array}{l}
{m_0}\left( {\frac{k}{{m + {m_0}}}} \right)\frac{{\left( {0,1 + \frac{{\left| q \right|E}}{k}} \right)}}{2} + \left| q \right|E = 0,5\\
\Leftrightarrow 0,3\left( {\frac{{10}}{{0,1 + 0,3}}} \right)\frac{{\left( {0,1 + \frac{{{{10}^{ - 4}}.E}}{{10}}} \right)}}{2} + {10^{ - 4}}.E = 0,5\\
\Rightarrow E = \frac{{{{10}^4}}}{{11}} = 909,1\left( {{\rm{V/m}}} \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Nguyễn Thị Thập
Copyright © 2021 HOCTAP247
