Hai nguồn sáng A, B dao động cùng pha cách nhau 8 cm.

* Hướng dẫn giải

​

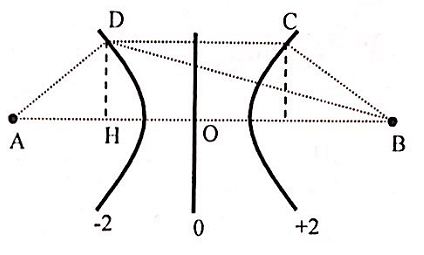
+ Vì hai nguồn cùng pha nên trung trực là cực đại. Để có 5 cực đại thì C và D nằm trên đường k = ±2.

+ Ta có: \({d_1} - {d_2} = k\lambda  \Leftrightarrow DA - DB =  - 2\lambda \) 

+ Từ hình:  

\(\begin{array}{l}
\left\{ \begin{array}{l}
DA = \sqrt {{2^2} + {{\left( {3\sqrt 5 } \right)}^2}}  = 7\left( {cm} \right)\\
DB = \sqrt {{6^2} + {{\left( {3\sqrt 5 } \right)}^2}}  = 9\left( {cm} \right)
\end{array} \right.\\
7 - 9 =  - 2\lambda  \Rightarrow \lambda  = 1\left( {{\rm{cm}}} \right)
\end{array}\)

+ Số đường dao động với biên độ cực đại trên AB:

\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow  - 8 < k < 8\) 

=> trên ΑΒ có 15 đường dao động với biên độ cực đại

+ Cứ 1 đường cực đại trên AB cắt đường bao ở 2 điểm nên trên đường bao ABCD có 15 x 2 = 30 điểm dao động với biên độ cực đại