Một con lắc lò xo gồm một vật nhỏ khối lượng 0,02 kg

* Hướng dẫn giải

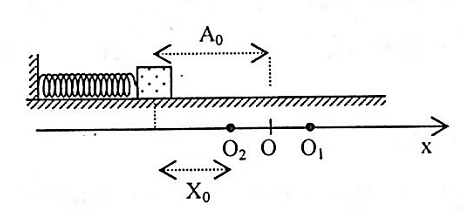
+ Vật sẽ đạt tốc độ cực đại khi đến O2. Tại vị trí này lò xọ nén đoạn:

\({x_0} = \frac{{\mu mg}}{k} = 0,02\left( m \right) = 2\left( {cm} \right)\) 

+ Áp dụng định luật bảo toàn năng lượng cho quá trình chuyển động từ vị trí thả đến vị trí O2, ta có:

 \(\begin{array}{l}
\frac{1}{2}kA_0^2 = \frac{1}{2}kx_0^2 + \frac{1}{2}mv_{\max }^2 + \mu mg\left( {{A_0} - {x_0}} \right)\\
 \Rightarrow v_{\max }^2 = \frac{k}{m}\left( {A_0^2 - x_0^2} \right) - 2\mu g\left( {{A_0} - {x_0}} \right)\\
 \Rightarrow v_{\max }^2 = \frac{k}{m}\left( {{A_0} - {x_0}} \right)\left[ {{A_0} + {x_0} - 2\mu g} \right]v_{\max }^2 = \frac{k}{m}{\left( {{A_0} - {x_0}} \right)^2}\\
 \Rightarrow {v_{\max }} = \sqrt {\frac{k}{m}} \left( {{A_0} - {x_0}} \right) = \sqrt {\frac{1}{{0,02}}} \left( {10 - 2} \right) = 40\sqrt 2 
\end{array}\)