Tại hai điểm A, B ở mặt chất lỏng có 2 nguồn kết hợp dao động điều hòa
Câu hỏi :
Tại hai điểm A, B ở mặt chất lỏng có 2 nguồn kết hợp dao động điều hòa theo phương thẳng đúng và cùng pha. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có nhũng điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm và NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?
A. 1,2 cm
B. 3,1 cm
C. 4,2 cm
D. 2,1 cm
* Đáp án
D
* Hướng dẫn giải
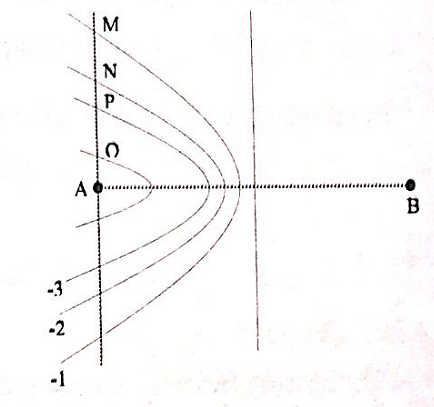
+ Vì M là điểm xa nhất nên M thuộc cực đại thứ nhất => kM = -1
+ Vì N, P là các cực đại kế tiếp nên => kN = -2; kP = -3
+ Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
MA - MB = - \lambda \\
NA - NB = - 2\lambda \\
PA - PB = - 3\lambda
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
\left( {22,5 + 8,75 + PA} \right) - MB = - \lambda \\
\left( {8,75 + PA} \right) - NB = - 2\lambda \\
PA - PB = - 3\lambda
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
MB = \left( {31 + PA} \right) + \lambda \\
NB = \left( {8,75 + PA} \right) + 2\lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 1 \right)\\
PA - PB = - 3\lambda
\end{array} \right.
\end{array}\)
+ Lại có:
\(\left\{ \begin{array}{l}
M{B^2} = {\left( {31 + PA} \right)^2} + A{B^2}\\
N{B^2} = {\left( {PA + 8,75} \right)^2} + A{B^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 2 \right)\\
P{B^2} = P{A^2} + A{B^2}
\end{array} \right.\)
+ Từ (1) và (2), ta có:
\(\begin{array}{*{20}{l}}
{\left\{ {\begin{array}{*{20}{l}}
{{{\left[ {\left( {31 + PA} \right) + \lambda } \right]}^2} = {{\left( {31 + PA} \right)}^2} + A{B^2}}\\
{{{\left[ {\left( {8,75 + PA} \right) + 2\lambda } \right]}^2} = {{\left( {PA + 8,75} \right)}^2} + A{B^2}}\\
{{{\left( {PA + 3\lambda } \right)}^2} = P{A^2} + A{B^2}}
\end{array}} \right.}\\
{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2\lambda \left( {31 + PA} \right) + {\lambda ^2} = A{B^2}}\\
{4\lambda \left( {8,75 + PA} \right) + 4{\lambda ^2} = A{B^2}}\\
{6.PA.\lambda + 9{\lambda ^2} = A{B^2}}
\end{array}} \right.\begin{array}{*{20}{c}}
{\left( 3 \right)}\\
{\left( 4 \right)}\\
{\left( 5 \right)}
\end{array}}\\
{\left\{ {\begin{array}{*{20}{l}}
{2\left( {31 + PA} \right) = 4\left( {8,75 + PA} \right) + 3\lambda }\\
{2\left( {31 + PA} \right) + \lambda = 9\lambda + 6PA}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\lambda = 4\left( {cm} \right)}\\
{PA = 7,5\left( {cm} \right)}
\end{array}} \right.}
\end{array}\)
+ Khoảng cách giữa hai nguồn AB:
\(AB = \sqrt {6.PA.\lambda + 9{\lambda ^2}} = 18\left( {cm} \right) \Rightarrow \frac{{AB}}{\lambda } = 4,5\)
+ Suy ra cực đại ngoài cùng gần A nhất ứng với kQ = -4
+ Ta có:
\(QA - QB = - 4\lambda \Leftrightarrow QA - \sqrt {Q{A^2} + {{18}^2}} = - 16 \Rightarrow QA = 2,125\left( {cm} \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Đình Xu
Copyright © 2021 HOCTAP247
