Đồ thị biểu diễn thế năng của một vật có m = 200g dao động điều hòa
Câu hỏi :
Đồ thị biểu diễn thế năng của một vật có khối lượng m = 200g dao động điều hòa ở hình vẽ bên ứng với phương trình dao động nào sau đây: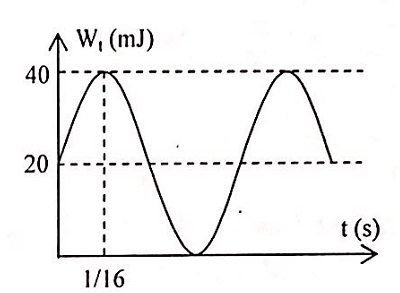
A. \(x = 5\cos \left( {4\pi t + \frac{{3\pi }}{4}} \right)\)(cm).
B. \(x = 5\cos \left( {2\pi t - \frac{\pi }{4}} \right)\)(cm).
C. \(x = 5\cos \left( {2\pi t + \frac{{3\pi }}{4}} \right)\)(cm).
D. \(x = 5\cos \left( {4\pi t + \frac{\pi }{4}} \right)\)(cm).
* Đáp án
A
* Hướng dẫn giải
+ Từ đồ thị thấy lúc t = 0 \( \Rightarrow {W_t} = \frac{W}{2} \Rightarrow x = \pm \frac{{A\sqrt 2 }}{2}\) và thế năng đang tăng nên vật đang đi đến vị trí biên.
+ Suy ra lúc t = 0:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{x_0} = \frac{{A\sqrt 2 }}{2}\\
{v_0} > 0
\end{array} \right.;\left\{ \begin{array}{l}
{x_0} = - \frac{{A\sqrt 2 }}{2}\\
{v_0} < 0
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
\varphi = - \frac{\pi }{4}\\
\varphi = \frac{{3\pi }}{4}
\end{array} \right.\\
x = \pm \frac{{A\sqrt 2 }}{2} \to \pm A\\
\Rightarrow \Delta t = \frac{T}{8} = \frac{1}{{16}} \Rightarrow T = 0,5\left( s \right) \Rightarrow \omega = 4\pi \left( {rad/s} \right)\\
W = \frac{1}{2}m{\omega ^2}{A^2} \Rightarrow A = 5\left( {cm} \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Hữu Trang
Copyright © 2021 HOCTAP247
