Con lắc lò xo treo thẳng, vật m1 ở vị trí cân bằng lò xo dãn 10cm.
Câu hỏi :
Con lắc lò xo treo thẳng đứng, vật dao động có khối lượng m1, khi ở vị trí cân bằng lò xo dãn 10cm. Đưa vật đến vị trí lò xo dãn 20cm rồi gắn thêm vật m2 = 3m1 bằng một sợi dây có chiều dài b = 10cm (xem hình vẽ), thả nhẹ cho hệ dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Khi hệ đến vị trí thấp nhất thì dây nối bị đứt, chỉ còn m1 dao động điều hòa, m2 vật rơi tự do. Bỏ qua khối lượng của sợi dây, bỏ qua kích thước của hai vật và bỏ qua ma sát. Lấy g = 10 = π2 m/s2. Sau khi đây đứt lần đầu tiền m1 đến vị trí cao nhất thì m2 vẫn chưa chạm đất, lúc này khoảng cách giữa hai vật là: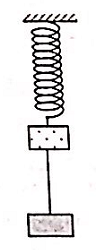
A. 2,3 m
B. 0,8 m
C. 1,6 m
D. 3,1 m
* Đáp án
C
* Hướng dẫn giải
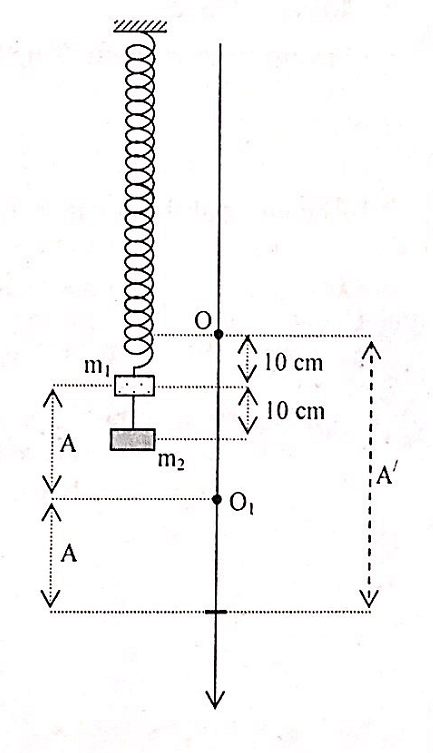
+ Lúc đầu chỉ có m1, tại VTCB O lò xo dãn 10cm
+ Đưa vật đến vị trí lò xo dãn 20cm thì vật ở dưới VTCB O đoạn x0 = 10 cm
+ Lúc này gắn thêm m2 = 3m1 thì VTCB của hệ bị dịch xuống đoạn: OO1 = 30 cm
+ Vậy, lúc này hệ ở trên VTCB O1 đoạn 20cm.
+ Do thả nhẹ nên hệ sẽ dao động với biên độ A = 20cm quanh VTCB O1.
+ Nhưng khi đến vị trí thấp nhất thì dây đứt, nên VTCB dịch về O.
+ Lúc này m1 cách O đoạn 50cm và có vận tốc bằng không nên nó sẽ dao động điều hòa quanh O với biên độ A/ = 50cm.
+ Khi m1 lên cao nhất thì đã đi được quãng đường s1 = 2A/ = 100 cm (kể từ vị trí đứt dây) và mất thời gian:
\(\Delta t = \frac{T}{2} = \frac{{2\pi }}{2}\sqrt {\frac{{\Delta {\ell _0}}}{g}} = \sqrt {0,1} \left( s \right)\)
+ Trong thời gian Δt này vật m2 rơi tự do nên quãng đường m2 đi được là:
\({s_2} = \frac{1}{2}g\Delta {t^2} = \frac{1}{2}.10.{\left( {\sqrt {0,1} } \right)^2} = 0,5\left( m \right) = 50\left( {cm} \right)\)
+ Vì dây dài b = 10 cm nên khoảng cách giữa hai vật lúc này là:
\(d = 100 + 10 + 50 = 160\left( {cm} \right) = 1,6\left( m \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Tô Ngọc Vân
Copyright © 2021 HOCTAP247
