Mạch điện xoay chiều gồm cuộn dây thuần cảm L, đoạn mạch X và tụ điện C
Câu hỏi :
Mạch điện xoay chiều gồm cuộn dây thuần cảm L0, đoạn mạch X và tụ điện có điện dung C0 mắc nối tiếp theo thứ tự trên. Điện áp hai đầu (L0, X) và hai đầu (X, C0) lần lượt là u1 và u2 được mô tả như đồ thị hình vẽ bên. Biết ω2L0C0 = 1. Điện áp hiệu dụng trên đoạn mạch X là: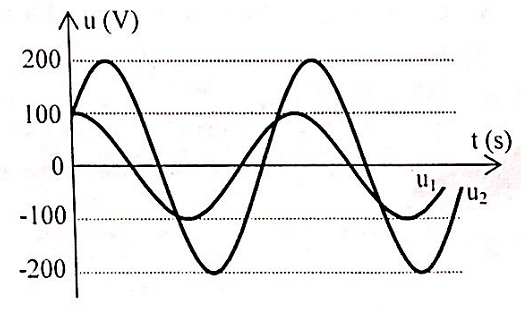
A. 50 √ 2V.
B. 100 √ 2V.
C. 25 √ 14V.
D. 25 √ 6V.
* Đáp án
C
* Hướng dẫn giải
+ Theo đề, ta có:
\({\omega ^2} = \frac{1}{{{L_0}{C_0}}} \Leftrightarrow \omega {L_0} = \frac{1}{{\omega {C_0}}} \Leftrightarrow {Z_L} = {Z_C}\) (1)
+ Từ đồ thị ta viết được biểu thức:
\(\left\{ \begin{array}{l}
{u_1} = 100\cos \omega t\left( V \right)\\
{u_2} = 200\cos \left( {\omega t - \frac{\pi }{3}} \right)\left( V \right)
\end{array} \right.\)
+ Vì uL và uC ngược pha nên
\(\frac{{{u_L}}}{{{U_{0L}}}} = - \frac{{{u_C}}}{{{U_{0C}}}} \Leftrightarrow \frac{{{u_L}}}{{{U_L}}} = - \frac{{{u_C}}}{{{U_C}}}{u_L} = - {u_C}\) (2)
+ Lại có:
\(\left\{ \begin{array}{l}
{u_{LX}} = {u_L} + {u_X} = {u_1}\\
{u_{XC}} = {u_X} + {u_C} = {u_2}
\end{array} \right.\left\{ \begin{array}{l}
{u_1} = {u_L} + {u_X}\\
{u_2} = {u_X} - {u_L}
\end{array} \right. \Rightarrow {u_X} = \frac{{{u_1} + {u_2}}}{2}\)
+ Theo đề, ta có:
\(\begin{array}{l}
{u_X} = \frac{{100 + 200\angle \frac{{ - \pi }}{3}}}{2} = 50\sqrt 7 \angle - 0,71\\
\Rightarrow {U_X} = \frac{{{U_{0X}}}}{{\sqrt 2 }} = \frac{{50\sqrt 7 }}{{\sqrt 2 }} = 25\sqrt {14} \left( V \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Tô Ngọc Vân
Copyright © 2021 HOCTAP247
