Đặt điện áp xoay chiều ổn định vào 2 đầu đoạn AB mắc nối tiếp (hình vẽ).
Câu hỏi :
Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB mắc nối tiếp (hình vẽ).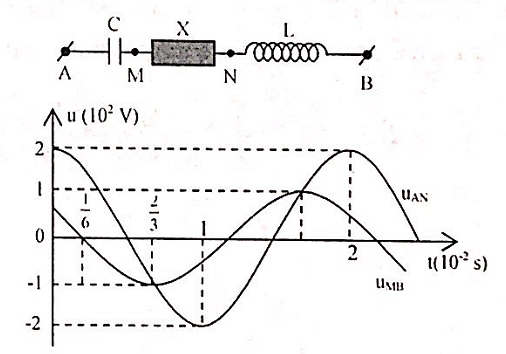
A. 173 V
B. 86 V
C. 122 V
D. 102 V
* Đáp án
B
* Hướng dẫn giải
Từ đồ thị, ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{U_{0AN}} = 200\left( V \right)\\
{U_{0MB}} = 100\left( V \right)
\end{array} \right.\\
t{\rm{ }} = {\rm{ }}0:\\
{u_{0AN}} = 200\left( V \right) = {U_{0AN}}\\
\Rightarrow {\varphi _{{u_{AN}}}} = 0 \Rightarrow {u_{AN}} = 200\cos \left( {100\pi t} \right)\left( V \right)
\end{array}\)
Còn uMB = 50V và đang giảm nên phương trình:
\(\begin{array}{l}
100\cos \left( {100\pi t + \frac{\pi }{3}} \right)V\\
\frac{{{u_L}}}{{{u_C}}} = - \frac{{{Z_L}}}{{{Z_C}}} = - \frac{2}{3} \Rightarrow {u_L} = - \frac{2}{3}{u_C}\\
\left\{ \begin{array}{l}
{u_{AN}} = {u_C} + {u_X}\\
{u_{MB}} = {u_X} + {u_L}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{u_{AN}} = {u_C} + {u_X}\\
{u_{MB}} = {u_X} - \frac{2}{3}{u_C}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
2{u_{AN}} = 2{u_C} + 2{u_X}\\
3{u_{MB}} = 3{u_X} - 2{u_C}
\end{array} \right.\\
\Rightarrow {u_X} = \frac{{2{u_{AN}} + 3{u_{MB}}}}{5} = \frac{{2.200\angle 0 + 3.100\angle \frac{\pi }{3}}}{5} = 20\sqrt {37} \angle 0,44\\
\Rightarrow {U_X} = 10\sqrt {74} V \approx 86V
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Khai Nguyên
Copyright © 2021 HOCTAP247
