1 công ty điện dùng đường dây tải điện với công suất truyền tải không đổi
Câu hỏi :
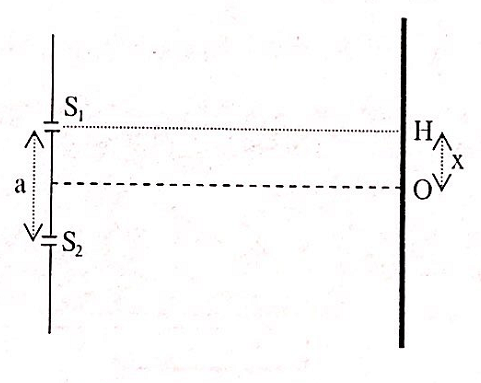
Cho thí nghiệm Y-âng, ánh sáng có bước sóng 500 nm. H là chân đường cao hạ vuông góc từ S1 tới màn M. Lúc đầu người ta thấy H là một cực đại giao thoa. Dịch màn M ra xa hai khe S1, S2 đến khi tại H bị triệt tiêu năng lượng sáng lần thứ nhất thì độ dịch là 1/7 m. Để năng lượng tại H lại triệt tiêu thì phải dịch màn xa thêm ít nhất là 16/35 m. Khoảng cách hai khe S1 và S2 là
A. 1 mm
B. 0,5mm
C. 1,8 mm
D. 2 mm
* Đáp án
D
* Hướng dẫn giải
+ Lúc đầu tại H là một vân sáng nên
\({x_H} = k\frac{{\lambda D}}{a}\) (1)
Sau khi dịch ra xa thêm 1/7 (m) thì H thành vân tối lần thứ nhất nên k giảm đi 0,5:
\({x_H} = \left( {k - 0,5} \right)\frac{{\lambda \left( {D + \frac{1}{7}} \right)}}{a}\) (2)
+ Dịch ra xa thêm 16/35 (m) thì H thành vân tối lần thứ 2 nên (k - 0,5) giảm đi 1:
\({x_H} = \left( {k - 1,5} \right)\frac{{\lambda \left( {D + \frac{1}{7} + \frac{{16}}{{35}}} \right)}}{a}\) (3)
+ Từ (1), (2) và (3), ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
kD = \left( {k - 0,5} \right)\left( {D + \frac{1}{7}} \right)\\
kD = \left( {k - 1,5} \right)\left( {D + 0,6} \right)
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
\frac{k}{7} - 0,5D - \frac{1}{{14}} = 0\\
0,6k - 1,5D - 0,9 = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
k = 4\\
D = 1\left( m \right)
\end{array} \right.\\
{x_H} = 0,5a = k\frac{{\lambda D}}{a}\\
\Rightarrow {a^2} = 2k\lambda D \Rightarrow a = \sqrt {2.4.0,5.1} = 2\left( {mm} \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Quốc Toản
Copyright © 2021 HOCTAP247
