2 chất điểm DDDH cùng tần số trên hai đường thẳng song song
Câu hỏi :
2 chất điểm DDDH cùng tần số trên hai đường thẳng song song kề nhau cách nhau 5 cm và cùng song song với Ox có đồ thị li độ như hình vẽ. Vị trí cân bằng của hai chất điểm đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết t2 – t1 = 3 s. Kể từ lúc t = 0, hai chất điểm cách nhau 5√3 cm lần thứ 2016 là: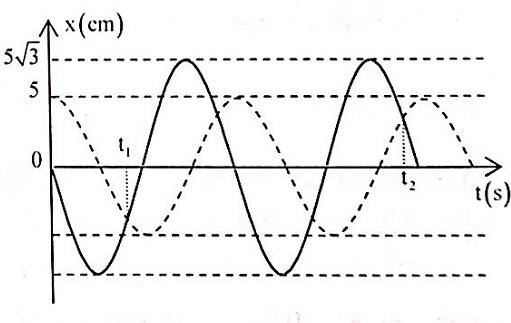
A. 12091/12s.
B. 6047/6s.
C. 2025/2s.
D. 12095/12s.
* Đáp án
A
* Hướng dẫn giải
+ Cứ sau nửa chu kì thì hai chất điểm lại đi ngang qua nhau.
+ Do đó, sau n lần ngang qua nhau mất thời gian: Δt = (n - 1)T/2
+ Từ đồ thị thấy trong thời gian 3 s chúng đi qua nhau 4 lần nên:
\(\left( {4 - 1} \right)\frac{T}{2} = 3 \Rightarrow T = 2\left( s \right)\)
+ Khoảng cách hai chất điểm theo phương dao động:
\(\Delta x = {x_2} - {x_1} = 10\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)\)
+ Trong một chu kì có 4 lần \(\left| {\Delta x} \right| = 5\sqrt 2 \left( {cm} \right)\)
+ Ta có:
\(\begin{array}{l}
\Delta t = \frac{T}{6} + \frac{T}{4} + \frac{T}{4} + \frac{T}{8} = \frac{{19T}}{{24}}\\
\Rightarrow t = 503T + \frac{{19T}}{{24}} = \frac{{12091}}{{24}}T = \frac{{12091}}{{12}}\left( s \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Quốc Toản
Copyright © 2021 HOCTAP247
